一种基于负数据库的隐私保护K最近邻分类算法毕业论文
2020-03-30 12:18:12
摘 要
负数据库是基于信息的负表示而提出的一种新型数据库,所谓信息的负表示就是使用原始数据在数据总集中的补集形式来表示原始数据。一个关于数据元素的数据集(DB)可以用它的补集来表示,称为负数据库(NDB)。由于负数据库采用的是原始数据的负表示的数据库,因此负数据库具有一定的安全性能。如果我们可以创造一个难以逆转出原始数据的负数据库,那么负数据库的安全性能就可以得到保障,可以实现信息的隐私保护。本文要做的就是创建一个难以逆转的负数据库实例,并且在不逆转负数据库的情况下实现一种KNN(最近邻分类)算法,就如标题所示,基于负数据库隐私保护的一种KNN算法。
关键字:负表示 负数据库 SAT公式 UCI数据集 KNN算法
Abstract
A negative database is a new type of database that is based on the negative representation of information. The negative representation of information represents the original data by using the complementary form of the original data. Negative databases have a certain security performance, because negative databases use the negative representation of the original data to replace original data. If we can create a negative database that is difficult to reverse, the security of the negative database can be guaranteed and the privacy of information can be protected. The purpose of this paper is to create a hard-to-reverse negative database instance and implement a KNN (K nearest neighbor classification) algorithm without reversing the negative database. As the title shows, implement a KNN algorithm based on the privacy protection performance of negative database.
Keyword:Negative representation.Negative database.SAT formula.UCI datasets .KNN algorith
目录
第1章 绪论 1
第2章 负数据库 3
1.1 负数据库的基本概念 3
2.2 生成负数据库 4
2.2.1 使用3-SAT公式构造负数据库 4
2.2.2 算法 5
2.3 负数据库的难解性与隐私保护 6
第3章 基于负数据库上海明距离估算的KNN分类 7
3.1 负数据库海明距离 7
3.2 负数据库海明距离的理论分析 7
3.3 基于海明距离的一种KNN算法 8
第4章 实验验证 9
4.1 训练集和测试集 9
4.1.1 数据集Tic-Tac-Toe Endgame Data Set 9
4.1.2 数据集Chess(King-Rook vs. King_Pawn) 10
4.2 实验结果及其分析 11
4.2.1 Tic-Tac-Toe Endgame Data Set 11
4.2.2 Chess(King-Rook vs. King-Pawn) 17
第5章 回顾与展望 19
参考文献 20
致谢信 21
第1章 绪论
近些年来负数据库以其良好的特性作为一种新型技术被运用到了信息安全以及隐私保护领域上[10]。所谓的信息的负表示,是受人工免疫系统启发而来。与传统的信息表示的区别在于信息的负表示是原始数据以其补集的数据的某种形式来表示[1]。也就是不在数据库的元素被表达,而数据库本身的内容没有被显示表达。由于由负数据库逆转求解出原始数据涉及到不确定性问题,是NP难的,因此负数据库作为一种信息负表示的存储形式,在信息安全和隐私保护具有独特的优势[10]。同时,负数据库还保留了传统数据库的一些基本操作,例如:选择、插入、删除、和更新等,保留了传统数据库操作简单的优点[1]。
K最近邻分类算法是一种很成熟的数据分类算法,自1968年由Cover和Hart提出[3],以其简单直观、分类准确的特点,受到了各领域关于处理数据挖掘分类工作的广泛应用[5]。同时,KNN分类算法的缺点也是十分的明显,但国内外的研究人员对K最近邻分类算法不断地改进,使其不断地适应大数据分析的要求。由此此次使用KNN分类算法的决定也是合理的。选择成熟的KNN分类算法使课题着重于隐私保护中的分类,而非单纯的分类算法的改良。
传统的KNN分类算法是基于原始数据的分类算法。传统的数据大多数是基于实值的,相对来说KNN分类算法简单直观,但是基于原始数据和实值分类不利于用户的隐私保护,可能造成数据的泄露。而负数据库还没有基于实值的[1],都是基于二进制字符串组成的数据库,而且还引入了不确定位。数据由于经过转换变得难以逆转,不再直观甚至意义模糊。因此基于负数据库的KNN分类算法是十分具有挑战性的。此次进行的课题意义,并非仅在于负数据库的某方面的深入研究,或者说KNN分类算法的在训练集和求近邻算法的优化,而是如何在保护隐私不降低信息安全性的情况下,即保持负数据状态不逆转甚至不了解数据含义的情况下,进行准确而安全的分类。这些尝试将会对负数据库信息安全和隐私保护产生积极地影响。
本次设计的目的在于实现或改进一种基于负数据库的隐私保护K最近邻分类算法。在查阅负数据库的相关文献时发现,国内对于负数据库方面的研究热度相对国外还是相对欠缺,只找到中国科技大学有相关优秀论文文献[11]。因此,希望此次在基于负数据库方面的研究,对与这种现象是有积极意义的。
在本文接下来的第二章中我们着重讲解了负数据库的基本概念和原理,讲述了负数据库的的一种生成方法,以及使负数据库难以逆转的要求,这是隐私保护性能的核心。第三章中我们主要提出和论证了基于负数据库的海明距离的算法,同时论证了使用负数据库海明距离估算任意二进制串与原始串的理论可行性。在第四章中我们进行了测试实验,找出了提高分类精度的规律。然后又进行验证实验,验证结论的正确性。最后我们在最后第五章做了总结以及一些后续工作展望。
符号列表:
s,y,v:二进制字符串。
wi:与原始数据有i位不匹配的二进制串。
U:数据库所有可能存在数据的全集。
DB:一组二进制字符串,称为正数据库。
U_DB:正数据库的补集。
NDB:压缩U-DB形成的一组使用{0,1,*}组成的字符串的集合,被称为负数据库。
NDB(s):字符串s的负数据库。
*:文中用作通配符,可同时代替位置上“0”和“1”,用来压缩数据集。
n:二进制串的位数。
m:负数据库中的记录数量。
r:负数据库中记录与字符串长度的比。
k:字符串中确定位置的数量(非“*”符号)。
第2章 负数据库
1.1 负数据库的基本概念
数据库可能大家都了解,就是按一定数据结构组织、存储和管理大量数据集合的仓库。其数据具有较低的冗余性,独立于应用程序,同时支持各种增删查改的基本功能。数据库的种种优点,加之信息时代数据爆炸的数据管理需求,使之在现代生活中无处不在。我们的生活、学习和工作中充满了形形色色、大大小小的数据库。
然而本文中的负数据库又是一种怎样的数据库呢?相对于传统数据库,负数据库的重点突出在一个“负”字,在这里“负”字代表的是信息的或数据的负表示。负表示其实是由人体免疫系统的负选择原理启发而而得到的一种数据表示方法,其核心在于使用数据的补集来表示数据,而不是直接的表示。就像人体内T细胞的成熟过程一样,与自身相匹配的T细胞会自动死亡,只有那些不相匹配的才能存活[1]。负数据库的形成就相当于T细胞的成熟过程,只有与原始数据不匹配的数据才能被负数据库选择,而与数据库相匹配的数则丢弃。
下面我们用数学语言以及一些例子来详细介绍一下负数据库。一个关于数据元素的数据集(DB)可以用它的补集来表示,称为负数据库(NDB)[10]。负数据库是基于二进制的数据库,基于实质的负数据库还有待开发。由上面符号列表,我们设DB是一个由n位二进制字符串组成的原始数据,U是所有n位二进制数据可能的全集,而U-DB是DB在全集U中的补集[1]。而NDB是DB补集U-DB的一种压缩形式,因为通常一个n位二进制字符串的补集U-DB是很大很耗费空间的,同时也是很容易逆转的。因此我们引入一个“0”和“1”的通配符,即在NDB字符串出现“*”的位置,可以同时与“0”和“1”相匹配。“*”所在的位置成为不确定位,因为我们不知道这个位置的具体值,反之已经由“0”和“1”确定的位置叫做确定位。因此,NDB可以说n为二进制DB在全集U下补集U-DB的以符号{‘0’、‘1’、‘*’ }来表示的一种压缩形式。我们几个例子,例如二进制串“0000”和“0001”:
表2.1 一个DB、U、U-DB和NDB的示例
DB | U | U-DB | NDB |
0000 0001 | 0000 0001 0010 0011 0100 0101 0110 1111 1000 1001 1010 1011 1100 1101 1110 1111 | 0010 0011 0100 0101 0110 1111 1000 1001 1010 1011 1100 1101 1110 1111 | 1*** *1** **1* |
上面是一个简单的示例,我们可以很清楚的看到U、U-DB和NDB之间的关系。上述的NDB是完备的,因为我们按照定义逆转NDB,正好可以得到DB{“0000”、“0001”}。而如果我们去掉NDB中的“1***”得到NDB{“*1**”、“**1*”},我们逆转得到的将是{“0000”、“0001”、 “1000”、“1001”}。里面有冗余串“1000”和“1001”,是不完备的。而我们需要尽量的生成完备的数据库,保持数据完整性。
负数据库根据原数据库二进制串的数量,可以分为单串数据库,两串数据库和多串数据库。例如图1.1的负数据库就是两串负数据库,因为DB中恰好只有两串数据。多串负数据库都可以由单串负数据库组来表达,如果不用单串负数据库组表达多串负数据库[1],也很容易通过改进单串负数据库生成方法来得到多串负数据库。而且在分类中,两者性质是一致的。为了简化数据,着重分析负数据库的性质和体现分类性能,在本文下面所讲的负数据库都是单串数据库。
2.2 生成负数据库
2.2.1 使用3-SAT公式构造负数据库
在文献[1]中我们可以知道,SAT公式与负数据库是等价的,而且逆转的难度也是等价的[1]。定义集合{x1,x2,x3,…xi…,xn-1,xn}是SAT公式布尔值集合。下标i表示在串中的位置,xi表示串第i位值的是肯定,值为1;i表示串第i位值的是否定,值为0。K-SAT表示由K个文字xi的SAT公式。所谓SAT公式就是被写做和取范式的布尔满足公式。
表2.2 一个简单的SAT公式示例
2-SAT | NDB | DB |
X1∨3 2∨X3 X1∨2 | 0*1 *10 01* | 100 101 111 000 |
在本文中我们采用的是3-SAT公式。显而易见的是,SAT公式的文字数过少是易解的,而文字数过多则会导致负数据库过大,两者皆不可取。1-SAT、2-SAT公式无论如可相对来说都是易解的,而4-SAT、5-SAT等等这些生成的负数据库过于庞大。因此我们选择3-SAT公式,既可以选择合适的算法生成难以逆转的负数据库,又可以控制负数据库的大小在可接受的范围内。
2.2.2 算法
生成负数据库和SAT公式有许多中方法,例如前缀算法、q-hidden方法、p-hidden方法、子句控制方法和前缀算法与q-hidden算法结合的混合算法等[1]。本文主要使用的是p-hidden算法,相比之下,p-hidden算法对于采用局部优先搜索策略的WalkSAT之类的求解器更加难解,而对于采用DPLL策略的求解器其求解难度是相当的[1]。接下来,我们就详细的描述一下p-hidden算法的具体步骤。
p-hiden(s,r,p1,p2) 输入:长度为n的二进制串; 限定r; 控制参数p1、p2。 输出:| NDB |=m的NDB 步骤: 1、令m=n*r,作为控制NDB大小的量度。 2、| NDB |lt;m时,以p1的概率生成与串s有一位不匹配位的串w1加入NDB;以p2的概率生成与串s有两位位不匹配位的串w2加入NDB;以1-p1-p2的概率生成与串s有三位不匹配位的串w3加入NDB。 3、当| NDB |=m时输出NDB。 |
在p-hidden算法中,我们通过控制参数p1和p2,以不同的概率生成了具有m=n*r条负记录的NDB。其中p1,p2是用来控制生成与二进制串s不相匹配的字符串wi(i={0,1,3},表示与s不匹配的位数)的比例的参数[1],由程序员自己输入。
2.3 负数据库的难解性与隐私保护
本文着重要实现的是基于负数据库隐私保护的KNN算法,而对于隐私保护,最重要的是得到的负数据库是难解的难以逆转的。如果负数据库容易被逆转,那隐私保护也就无从谈起。反而浪费大量空间和时间,得不偿失。
而在负数据库发展的过程中q-hidden方法、p-hidden方法、子句控制方法这些都被证明在选择合适参数的时候,对于WalkSAT求解器(采用局部优先搜索策略,是不完备的)和采用DPLL策略(是一种完备的、以回溯为基础的算法,用于解决在合取范式中命题逻辑的布尔可满足性问题)的求解器是难解的[1]。(详细算法及其难解性证明可见文献[1],这里就不一一赘述了。)
在上述我们采用的p-hiden算法可以生成负数据库,但是要生成难以逆转的负数据库,对参数p1、p2是有要求的。
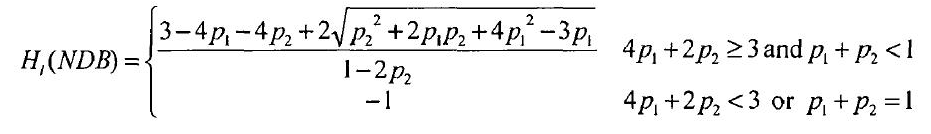
图2.1 p-hidden算法难以逆转的条件[1]
Hi(NDB)表示的是生成的负数据库难以逆转的程度, “-1”说明负数据库是容易逆转的,Hi(NDB)的值越大说明负数据库是越难解的[1]。一般来说我们认为Hi(NDB)gt;0,NDB就是难解的。至于公式的证明,详细过程就参见文献[1]中的第三章,这里就不做证明了。
而对于p-hidden中的限定r,其实也是有要求的。一般来说,取rgt;5.5,生成的负数据库是难以逆转的[1]。但是也不能将r取的过大,使负数据库的数据过于庞大。不利于进行其他的工作。
第3章 基于负数据库上海明距离估算的KNN分类
3.1 负数据库海明距离
到分类,最重要的是采用何种方式或者距离,来表示样本之间的相似程度。合适的方法,可以得到较为精确的分类效果。对于基于数值的分类,我们一般采用欧氏距离。但负数据库之间计算欧氏距离是十分复杂的,而且在证明上难度较大。故我们选取计算较为简单,对于串之间的相似程度描述较为精确的海明距离。
海明距离是指两个码或者字符串之间对应位置不相同的个数。而二进制串s与负数据库之间的海明距离的算法与之也是大同小异。设串w∈ NDB,w中的不确定位“*”对于串s和NDB之间海明距离的贡献为0。而当串s与串w对应位相匹配时,海明距离 1。而当串s与串w对应位不相匹配时,海明距离-1。直到遍历玩NDB中所有的串w,求得的海明距离即为串s与NDB之间的海明距离。下面请看详细算法[1]:
HaiminDist(s,NDB) 输入:二进制串s,负数据库NDB。 输出:海明距离H(s,NDB)。 步骤:1、设串w∈ NDB。 2、对于所有w∈ NDB,计算w与s之间的海明距离,并相加。计算方法为w中的不确定位“*”对于串s和NDB之间海明距离的贡献为0。而当串s与串w对应位相匹配时,海明距离 1。而当串s与串w对应位不相匹配时,海明距离-1。 3、输出NDB。 |
下节将证明,负数据库与串s采用此种方法求出来的海明距离,可以用来近似估计逆转负数据库得到的原始数据与串s之间的海明距离。
3.2 负数据库海明距离的理论分析
这一节,我们来讨论一下使用任意串与p-hidden算法生成的负数据库海明距离来估算此串与负数据库原始数据之间海明距离的合理性。设s为一个长度为n的二进制串,NDBs为使用p-hidden算法生成的负数据库,pi为p-hidden算法确定位中不匹配位的控制参数,i表示确定位与s的不匹配位数。同时,NDBs的大小为m=r*n。v为一个长度为n的任意二进制串,j为二进制串s与v之间的不同位个数(也是两者之间的海明距离H(s,v))。




