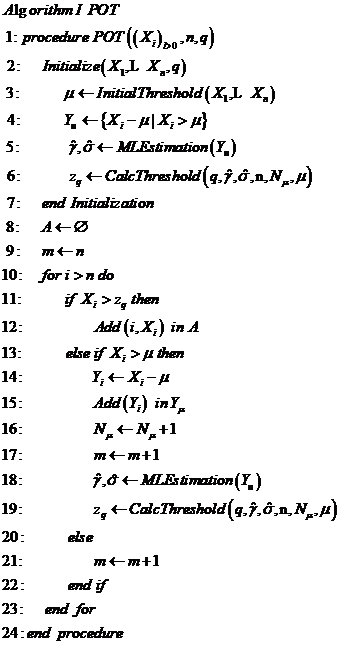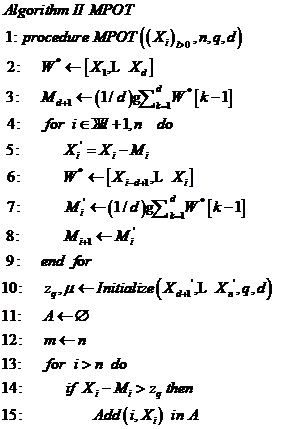摘 要

大型互联网公司需要密切监控其web应用的各种运维数据，如页面浏览量、在线用户数量和订单数量等。这通常被称为关键性能指标（KPI），是典型的时序数据。对此进行时序数据异常检测，可以判断系统是否出现异常行为，是保障系统安全稳定运行的重要手段，兼具商业价值和科研价值。

本文分析了运维环境中时序数据异常检测的三种模型：平稳型、不稳定型和周期型，提出了一种基于极值理论的单变量周期型时序数据异常值检测的方法，包含异常检测模块和LSTM神经网络预测模块。该方法不需要手动设置阈值，也不需要假设分布，很好的控制了假阳性，可用于多种情况的异常检测。

真实KPI数据集上的实验显示我们的方法比一些经典算法具有更高的有效性和准确率。同时，我们的方法具有通用性，可以很好地应用于其他时序数据异常检测领域。

关键词：异常检测；极值理论；KPI；时序数据；长短期记忆神经网络

Abstract

The importance of anomaly detection in time series in many practical applications, it had attracted considerable attention, including fault detection, network intrusion detection, energy management and finance, etc. In this thesis, we mainly solved the problem of outliers of KPI time series data based on dimension environment. Nowadays, most approaches for detecting outliers rely on either manually set thresholds or assumptions on the distribution of data, in addition, the boundary between normal and anomalous behavior is often not precise, causing a high false positive rate.

In this thesis, we proposed a new method based on Extreme Value Theory to detect outliers of periodic KPIs, including anomaly detection module and LSTM neural network prediction module. This method does not require to hand-set thresholds and makes no assumption on the distribution, controls the number of false positives, also be used for anomaly detection in a variety of situations.

Finally, we also experimented with algorithms on real datasets with labels from KPI anomaly detection competition, which proved the correctness and effectiveness of our method. We also conducted comparative experiments with some classic algorithms, the experimental results showed that our solution had higher practicability and accuracy in the anomaly detection of periodic KPIs.

Key Words：anomaly detection; Extreme Value Theory; KPI; time series data; LSTM

目 录

摘 要 I

Abstract II

第1章 绪论 1

1.1 研究背景 1

1.2 国内外研究现状 1

1.3 研究内容和技术路线 2

1.3.1 研究内容 2

1.3.2 技术路线 4

1.4 论文的创新点 5

1.5 论文结构安排 5

第2章 极值理论 7

2.1 什么是异常值 7

2.2 极值理论 7

2.3 广义Pareto分布 9

2.4 本章小结 9

第3章 平稳型时序异常检测模型 10

3.1 POT模型 10

3.2 极大似然估计法 10

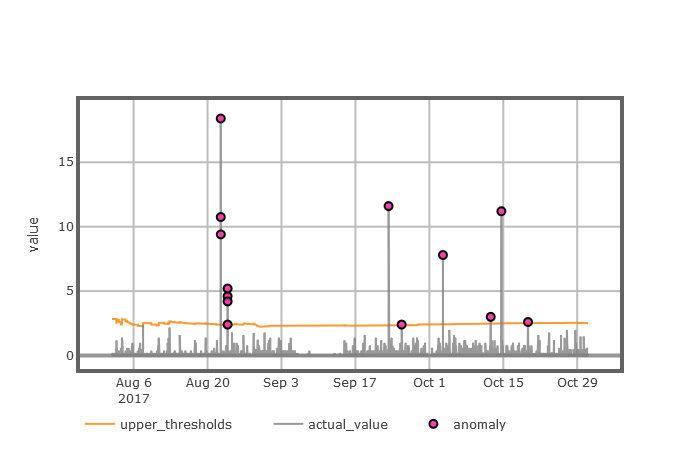
3.3 POT模型异常检测实例分析 11

3.3.1 POT模型异常检测算法 11

3.3.2 实例分析 13

3.4 本章小结 13

第4章 不稳定型时序异常检测模型 14

4.1 POT模型存在的问题 14

4.2 MPOT模型 14

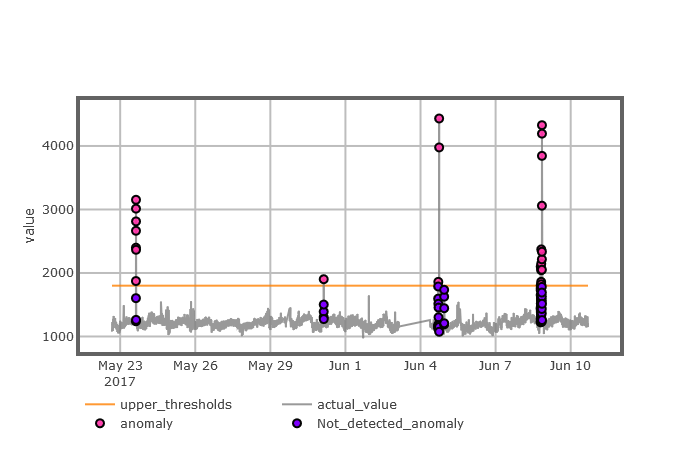
4.3 MPOT模型异常检测实例分析 15

4.3.1 MPOT模型异常检测算法 15

4.3.2 实例分析 17

4.4 本章小结 18

第5章 周期型时序异常检测模型 19

5.1 MPOT模型存在的问题 19

5.2 LSTM时序预测 19

5.2.1 人工神经网络（ANN） 20

5.2.2 递归神经网络（RNN） 20

5.2.3 LSTM及算法 20

5.3 LMPOT模型异常检测实例分析 23

5.3.1 LMPOT模型异常检测算法 23

5.3.2 实例分析 25

5.4 本章小结 26

第6章 实验和结果 27

6.1 数据集 27

6.2 LMPOT模型的有效性分析 27

6.3 ROC曲线 28

6.4 主要参数(q)分析 30

6.5 对比实验结果分析 30

6.6 本章小结 32

第7章 结论与展望 33

7.1 结论 33

7.2 展望 33

参考文献 34

致 谢 36

第1章 绪论

本章首先介绍了课题的背景、及意义，然后围绕国内外的研究现状，提出了本文的研究内容和技术路线，最后对论文的总体结构做了简单的介绍。

1.1 研究背景

现如今随着互联网特别是移动互联网的飞速发展，web服务已经深入到了社会的各个领域，即人们使用互联网进行搜索、购物和娱乐等等。为了确保业务不间断，大型互联网公司需要密切监控其web应用的各种运维数据，其中，关键性能指标（Key Performance Indicator, KPI）是实时判断web服务是否稳定的重要风向标之一，一直受到广泛的重视。KPI是时间序列数据，衡量诸如页面浏览量、在线用户数量和订单数量等指标。 在所有关键绩效指标中，大多数是与业务相关的关键绩效指标，这些关键绩效指标受用户行为和时间安排的严重影响，因此大致具有定期发生的季节性模式（例如每天或每周）。然而，对于具有各种模式和数据质量的这些周期型KPI的异常检测一直是一个巨大的挑战，通过算法分析运维环境中的真实KPI时间序列数据，以准确检测异常情况并及时排除触发的故障，判断系统是否出现异常行为，保证系统稳定运行，这同时兼具商业价值和科研价值。

通过对该课题的研究，针对单变量周期型KPI时序数据设计出一个较为高效准确的异常检测算法来提高检测效果，运用于KPI时序数据的异常值检测，确保系统业务的正常进行。同时，希望我们提出的方法可以应用于多种场景，包括安全入侵检测、气象预测、金融管理等等，体现本次课题研究的意义和价值。

1.2 国内外研究现状

如何对时间序列数据进行异常值检测，引起了国内外学术界和工业界的重视。在时序数据方面的异常检测研究，由于数据的特征不同且存在各种各样的曲线类型，且数据维度也存在单变量和多变量的区别，针对异常检测算法类别可以分为以下几种类型：

基于统计的方法：即对于给定的数据集，我们先假设一个分布（比如高斯分布等），根据假设的分布用不一致性测试识别数据中的异常情况。基于统计方法的异常检测具有一定的局限性，主要是因为我们事先要知道数据的具体分布特征，然而往往数据服从的具体分布未知，所以这类方法的应用效果并不好。基于距离的方法：这种方法简单的来说就是检测到的异常点远离大部分数据，没有足够多的 “邻居”。基于距离的方法跟基于统计的方法相比，基于距离的方法的异常情况更符合Hawkins的异常本质定义（定义见2.1节）。基于偏差的方法：这种方法提出的是一种“序列异常”的概念。对数据集合拆分成一系列有序子集，根据该子集与前序子集的偏差来确定异常；基于密度的方法：数据之间的密度估计可以相对直接通过计算得到，高密度区域中的对象相对接近近邻，可以看做为正常，而低密度区域中的对象相对远离近邻，可以看做为异常。

目前存在针对于各种时序数据特征的异常检测算法，可以分为以下类型及对应存在的解决办法：

1）针对平稳型时序数据的异常检测方法，这种数据在整体上趋于平稳，但局部会出现一些大的波动，可以使用静态阈值方法^[1]进行检测，该方法使用恒定的阈值解决，一旦异常点超过既定阈值就判定为异常。还有些用于评估平稳型时间序列的趋势的方法，如移动平均法^[1]、权重移动平均法^[3]、Holtwinter^[4]，简单来说就是用数值前后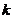个时间点的值的平均值来代替当前值；ARIMA方法^[5]，这种方法对于平稳型的时序数据效果较好，但是只适用于季度或者月份为季节性的稳定时间序列数据；

2）针对不稳定型时序数据的异常检测方法：现阶段的方法是采用极值理论^[6]的思想来检测，通过调整参数来检测异常。还有种方法是通过使用wavelet filters^[7]去检测局部数据的方差来达到检测异常值的效果；

3）针对周期型时序数据的异常检测方法：这种数据具有很强的周期性、季节性以及趋势，现在比较流行的方法是建立预测模型和报警模型，先对时序数据进行预测，然后再根据概率统计方法建立报警模块，并根据这个报警模块对相应时序数据做出预报或判断。还有无监督异常检测^[8]的机器学习方法应用于周期型时序数据的异常检测。

以上是目前国内外存在的一些解决时序数据异常检测的方法，但是它们的异常检测算法仅是针对特定类型的时序数据，然而在面对时序数据的异常种类、曲线的多样性、时序异常检测参数配置成本高等问题时，是否存在一个通用的、不需要调参数的异常检测系统呢？针对这类难题设计，清华大学NetMan实验室近期在异常检测领域的研究成果：基于机器学习的KPI自动化异常检测系统^[9]，该系统通过将机器学习中的监督式分类方法成功应用于异常检测的问题上，解决了异常检测算法参数调整的复杂难题，实现了自动化的异

常检测框架。

KPI时序数据的异常检测在实际工业系统中越来越重要。主要是因为各种工业监控系统存在不同类型的KPI时序曲线需要维护，为保证系统的正常运行，所以为不同类型的KPI时序曲线设计合理的异常检测算法显得尤为重要。

1.3 研究内容和技术路线

1.3.1 研究内容

本文围绕单变量时序数据的异常检测这一主题，提出了基于极值理论的周期型时序数据异常检测方法，并以单变量的KPI时序数据为研究对象，具体内容包括以下几个部分：

1）单变量的KPI时序数据的选取；本文采用的真实时序数据，在数据的选取方面分为三种类型，即平稳型KPI时序数据、非平稳型KPI时序数据以及周期型KPI时序数据，选取合适数据做异常检测以验证方法的有效性；

2）时序数据异常值的判断；通过研究现有的基于极值理论的方法来刻画异常值的行为，对现有模型和方法进行改进，通过引入LSTM神经网络以建立周期型时序数据的异常值检测方法；

3）LSTM神经网络对周期型的时序数据进行预测；通过预测同时期的数据以保证数据具有的季节性、趋势等，在模型检测到异常值时使用预测的同时期数据进行阈值更新；

4）根据我们提出的异常值检测模型，选取相应的时序数据集进行案例分析，并对模型的算法进行评估；本文的研究内容简图如图1.1所示：

图1.1 本文研究内容

1.3.2 技术路线

本文中，我们基于极值理论的思想来对单变量时序数据进行异常值检测，并以KPI时序数据为基础，通过分析和处理，我们根据数据与时间的分布关系主要将时序数据分为以下三类：平稳型（数据分布和时间无关）、不稳定型（数据分布和时间呈弱相关）以及周期型KPI时序数据（数据分布和时间呈强相关），然后针对这三种类型我们通过借鉴并改善现有基于极值理论的异常检测模型，通过对模型的不断更新，我们最后提出了针对周期型时序数据的异常检测新模型。具体的技术路线图如图1.2所示：

图1.2 技术路线图

1.4 论文的创新点

本文提出了周期型时序数据异常值检测的新方法，包含异常检测模块和LSTM神经网络预测模块，故具有如下几点创新点：

1）对现有基于极值理论的异常检测方法借鉴并加以改进；

2）引入LSTM神经网络对KPI时序数据进行预测，并融合现有的基于极值理论的异常检测方法；

3）提出新的异常值判断策略，在检测到异常值时使用LSTM预测的同期数据进行阈值更新以保证阈值能够跟随周期型数据的趋势和周期性；

4）同时论文还研究了不同模型在不同类型的时序数据集上的表现，更加细分了模型的有效性和准确性。

1.5 论文结构安排

本文围绕以KPI时序数据的背景、异常值检测的目的和意义、极值理论、移动平均法和LSTM神经网络等方面，全面介绍了KPI时序数据异常值检测的研究内容及技术路线。通过分别对平稳型、不稳定型和周期型KPI时序数据进行检测，一步一步逐渐完善我们的模型，并且用真实的KPI时序数据来测试我们的解决方案的有效性，最后通过与现在一些经典的算法进行比较来评估我们的算法。全文共分为六个章节：

第1章：绪论，主要介绍了毕设课题的研究背景、意义，并对时序数据异常值检测的发展历程和国内外发展现状进行介绍，提出课题的研究内容、技术路线及论文结构安排。

第2章：极值理论，该章首先介绍了时序数据异常值的定义，紧接着对极值理论和广义Pareto分布进行了详细介绍，为我们在第三章中建立的初步模型奠定理论基础。

第3章：平稳型时间序列异常检测模型，该章主要介绍了如何运用我们在上一章中描述的极值理论来刻画异常值的渐近行为，以此得到了平稳型时序模型(POT)，然后使用极大似然估计法来求解POT模型的相关参数，最后用带有异常标注的真实的平稳型KPI时序数据对POT算法的进行有效性分析。

第4章：不稳定型时间序列异常检测模型，该章主要介绍了POT模型运用到不稳定型的KPI时序数据的异常检测上所发现的问题及原因，通过引入移动平均法对POT模型进行更新，得到不稳定型时间序列模型(MPOT)，最后用带有异常标注的不稳定型KPI时序数据对MPOT算法进行有效性分析。

第5章：周期型时间序列异常检测模型，该章主要介绍了MPOT模型运用到周期型的KPI时序数据的异常检测上所发现的问题及原因，因此我们引入LSTM预测模块对MPOT模型进行改进，提出了周期型时间序列模型(LMPOT)，最后用带有异常标注的周期型KPI时序数据对LMPOT算法进行有效性分析。

第6章：实验和结果，该章主要介绍了LMPOT模型的性能，然后通过与现有的一些经典的时序数据异常检测算法进行对比实验，结果表明了我们的方法在检测周期型时序数据上具有更高的实用性和准确性。

第7章：结论与展望，该章主要介绍了本文的结论，即提出了一种在周期型时间序列数据中检测异常值的新方法，紧接着在理论层面和实践层面上对我们的方法进行了拓展和展望，希望我们的方法可以应用到更多方面，解决更多的问题。

第2章 极值理论

在这一章里，我们将简单介绍时序数据异常值的定义、极值理论及极值统计模型之一的广义Pareto分布。

2.1 什么是异常值

什么是异常值？Hawkins(1980)给出了异常的本质性的定义：异常是在数据集中与众不同的数据，使人怀疑这些数据并非随机偏差，而是产生于完全不同的机制^[10]。我们可以暂称其为存在数据中的一种不符合正常行为的模式。图2.1中显示了简单的二维数据中的异常情况，由于某种原因导致数据的分布如图所示。数据有两个区域即normal区域和outlier区域，因为大部分数据分布在normal区域（如图中的红色区域），所以我们认定normal区域为正常区域，outlier区域的点（如图中的outlier_1、outlier_2、outlier_3、outlier_4这四个点）距离正常区域足够远，所以我们认定outlier区域的点是异常的。

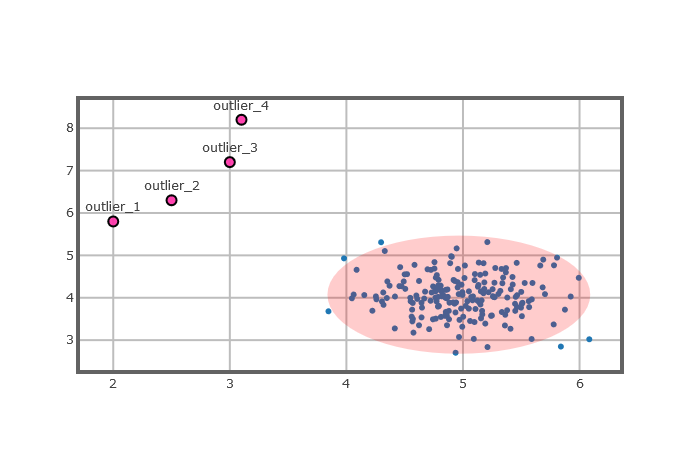
图2.1 一个简单的异常值分布示例

时间序列中的异常检测由于其在许多实际应用中的重要性而引起了相当大的关注，包括入侵检测，能源管理和金融等，这些数据中都可能会引发异常情况，而本文我们主要讨论的是基于运维环境下的单变量KPI时序数据的异常情况。

2.2 极值理论

极值理论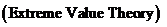是1943年由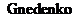^[12]提出，是统计学理论的一个分支，目前在气象、地震和金融风险等领域有着较广泛的应用。从极值理论研究的对象和范围可以看出，极值理论很适合用来研究时序数据方面的异常检测问题。

一元极值理论：假设存在随机变量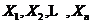，它们是独立同分布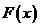，为其总体分布函数，将这组独立同分布的样本按照顺序排列，有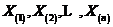，则称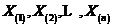为次序统计量。然后令：

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：