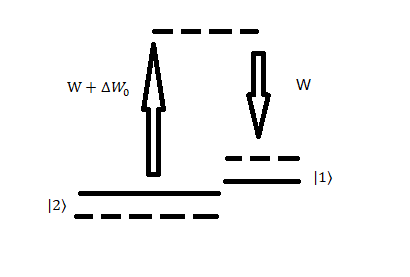摘 要

实验人员们在近几年通过人工规范势和自旋—轨道耦合相互作用，实现了在中性原子中的自旋角动量和轨道角动量的耦合，发现了在自旋轨道耦合的作用下，会带来一些新的效应，这为量子力学，量子光学，凝聚态物理，量子少体，拓扑超流系统等众多领域带来了新的研究阵地，它许多的基本物理现象中扮演了重要角色，也成为了新奇量子物态里不可或缺的一环。

本文将从自旋轨道耦合的起源出发，介绍了自旋轨道耦合的研究背景和意义，以及自旋轨道耦合的国内外发展现状及发展前景。

而原理的部分则从狄拉克方程开始，通过粒子在人在规范场的运动，介绍自旋轨道耦合的原理。并把自旋轨道耦合分为真空与腔内两种研究方向，利用双拉曼光进行自旋轨道耦合在真空的实现，再用一个光学腔代替其中一束拉曼光，用量化的光场实现腔内冷原子自旋轨道耦合的研究。

在关于能级曲线的分析中，本文通过用编程软件对真空和腔内的原子自旋轨道的计算，从而得到其能量与动量之间的关系，通过改变相关的参数研究和分析它们对自旋轨道耦合的影响。

最后本文进行了总结和展望。对于本次自旋轨道耦合的研究，使得本人对自旋轨道耦合有了一个初步的了解，并通过对其能级的色散关系的分析，进一步学习了自旋轨道耦合的相关知识及效应，更加深入地觉察到了自旋轨道耦合所带来的研究前景。

关键词：自旋轨道耦合；冷原子；能级分析

Abstract

In recent years, experimenters have found the interaction between artificial gauge potential and spin-orbit coupling (SOC), completed the coupling of spin angular momentum and orbital angular momentum in neutral atoms, and found that under the effect of spin-orbit coupling, some new effects will be brought, which will bring about quantum mechanics, quantum optics, condensed matter physics, quantum few bodies, topological flow superfluid system, etc. Many fields have brought new research positions, which play an important role in many basic physical phenomena and become an indispensable part in novel quantum states.

Starting from the origin of spin-orbit coupling, this paper introduces the research background and significance of spin-orbit coupling, as well as the development status and prospects of spin-orbit coupling at home and abroad.

The principle of spin-orbit coupling is introduced from Dirac equation through the motion of particles in the gauge field. The spin-orbit coupling is divided into two research directions: vacuum and cavity. The spin-orbit coupling is realized in vacuum by using double Raman light. Then an optical cavity is used to replace one of the Raman light beams and quantized light field is used to realize the spin-orbit coupling of cold atoms in the cavity.

In the analysis of the energy level curve, the relationship between energy and momentum is obtained by calculating the spin orbits of atoms in vacuum and cavity by programming software, and their effects on the spin orbit coupling are studied and analyzed by changing the relevant parameters.

The last part is the summary and Prospect of this paper. For this spin-orbit coupling research, I have a preliminary understanding of the spin-orbit coupling. Through the analysis of the energy level dispersion relationship, I further learned the spin-orbit coupling knowledge and effects, and more deeply perceived the research prospects of spin-orbit coupling.

Keywords: Spin-orbit coupling (SOC); Cold atoms; Energy level analysis

目 录

第1章 绪 论 1

1.1 研究背景和意义 1

1.2 国内外研究发展现状 1

1.3 本文研究内容 3

第2章 自旋轨道耦合原理 5

2.1 狄拉克方程 5

2.2 规范场与自旋轨道耦合 6

2.3 电子的自旋轨道耦合 6

2.4 原子的自旋轨道耦合 7

2.5 小结 7

第3章 双拉曼光的自旋轨道耦合的实现 8

3.1 人造规范场的建立 8

3.2 哈密顿量 9

3.3 仿真结果分析 10

3.3.1 无失谐，无耦合强度的情况 11

3.3.2 无失谐的情况 11

3.3.3 有失谐的情况 12

3.3.4 仿真结果对比 12

3.4 小结 13

第4章 腔内冷原子的自旋轨道耦合的实现 14

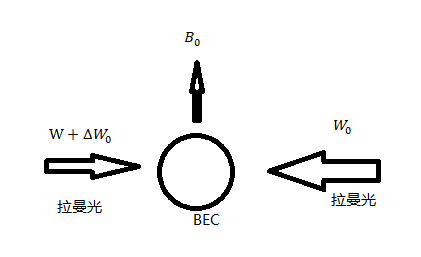
4.1 腔内人造规范势的建立 14

4.2 腔内哈密顿量 15

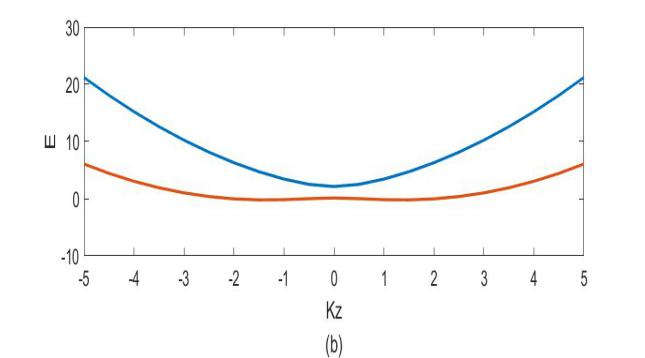
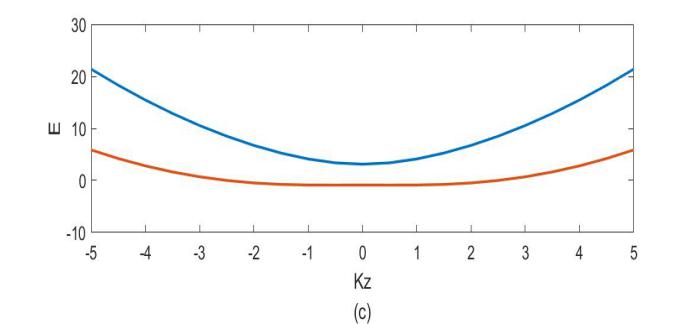
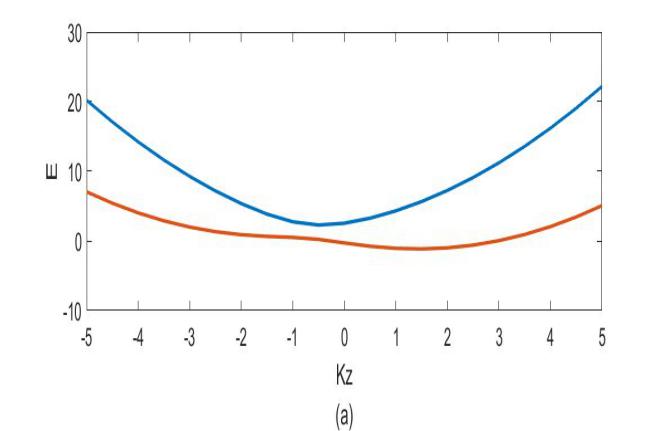
4.3仿真对比分析 16

4.3.1 无失谐的情况 16

4.3.2 失谐为正的情况 17

4.3.3 失谐为负的情况 18

4.3.4 仿真对比分析 19

4.4 小结 20

第5章 总结与展望 21

5.1 本文总结 21

5.2 展望 22

参考文献 23

致谢 25

第1章 绪 论

1.1 研究背景和意义

自从伟大的物理学家爱因斯坦预言在超低温会形成一种特殊的凝聚体——玻色-爱因斯坦凝聚体（BEC），关于冷原子的研究就成为了一个新的大陆，等待着科学家们去探索。

冷原子的优点不胜枚举，如冷原子的纯度良好并且拥有相互作用的可调节性，且原子在超冷情况下，我们有很多种方式可以精确操控量子多体的系统，因而冷原子各种不胜枚举的优势为科学家们的探索和攀登带来一个新的思考方向和前进的指引。自从那个时候开始，有关于冷原子方面的研究便坐上了高速快车，在短暂的几十年内蓬勃开花。特别是费什巴赫共振、光学晶格和人工规范势等高灵敏度量子控制技术的实验取得了很大进展，它已成为许多领域何许多新型材料的主要研究前沿阵地^[15]。

自旋轨道耦合，即SOC，几乎存在于所有的材料之中,它自旋电子学中是一个很重要的相互作用。在某些材料之中，其粒子的自旋轨道耦合的作用十分薄弱，但是有的材料之中的自旋轨道耦合的作用比较强烈，不能忽视，它甚至会影响粒子的能级色散曲线，影响粒子一些性质的变化。因此在很多研究中，粒子的自旋轨道耦合成为了不可省略并且需要重视的地方，关于粒子的自旋轨道耦合的一些计算对总体的结果往往会产生较大的影响。

而最近在中性原子中，人们通过建立相应的人造规范势，成功实现了用人造规范势中的中性原子的远运动来模拟电子的自旋轨道耦合，这个实验的成功为其他有关SOC的延伸或者交叉运用提供了新的思路。在量子光学力学中，SOC是一种比较基本但也容易被忽视的一种物理现象。研究表明，自旋-轨道耦合可以带来一系列新奇物理现象。如：人们发现在自旋-轨道耦合的存在下，冷原子之间的相互作用发生了改变；自旋-轨道耦合可以使两体散射的波函数的短程行为发生改变，引起混合分波散射，又如，把光子的SOC应用到纳米级这个层次，从而改变光子的自旋信息的处理。

总的来说，冷原子的一些在研究方面的特点和模拟场建立比较有优势，十分适合作为模拟腔内粒子自旋轨道耦合的研究对象。

1.2 国内外研究发展现状

到现在为止，冷原子研究成为了世界上科技强国们的香饽饽。以美国为例，为了能在冷原子研究领域占得先机以及优势，哈佛-麻省理工学院，JILA研究所，斯坦福大学，杜克大学等等一系列世界知名学府都成为了冷原子世界的开拓者。来自欧洲的英国剑桥大学，瑞士苏黎世理工，意大利佛罗伦萨LENS等也不甘示弱，加大了对冷原子方面的投入及研究。甚至一些亚洲国家，也加入了这场竞争。

NIST的Spielman实验小组研究成果比较突出，他们采用拉曼光的耦合使得建立的人造规范场和电磁场成功耦合从而用中性原子模拟了电子的自旋轨道耦合。而在玻色-爱因斯坦凝聚态中进行人造规范势和相应的中性冷原子自旋轨道耦合这个实验可以十分明确且清晰地解释自旋轨道耦合这个模型平台，给科学家们探索新的有关量子的物理现象提供了许许多多的有利资源。且并不止于此，最近科学家们在这个成功案例之上，延伸出了很多很多充满想象力的SOC模型，并且也构造了一些比较新颖的拓扑结构。尽管这些开拓式的想法由于种种实际性的原因并没有被于现实里被实现，可是这些宝贵的理论，数据以及进步的研究方向将会指引着科学家和研究人员们奋勇向前。

实验的可控制性一直是实验能否有说服力的一项重要标准，由于使用中性冷原子来模拟电子的自旋轨道耦合的成功实验，这标志着关于SOC等的一些新奇的物理现象现在可以在科学家们控制下进行研究。但是由于超冷原子气体的组成是好几十万的粒子的叠加，所以关于量子多体的问题便成为了十分棘手的挑战。

可是科学家们前进的步伐从来不会被困难所阻挡。十一年前，美国，一个叫做檀时钠的科学家在挑战量子多体这拦路虎的过程之中，运用充满想象力又不失理性的思维，提出了著名的接触理论。檀时钠在他的研究之中，创造性地在自旋轨道耦合这个系统之中，融入了他自己的接触理论，并也得到并且研究了在冷原子系统之中，那些短程性相互作用的粒子之间的种种普适性关系。也正如檀时钠研究发现的那样，自旋轨道耦合这个系统之中，我们可以采用新的量得到体系中诸如动量，波函数等等一系列的关系的渐进行为。所以，檀时钠教授的研究为开辟了一条有关于SOC体系普适性的研究的道路，为科学家们SOC的研究方向上提供了更多的选择。

图1.1 含自旋轨道耦合和拉比耦合的BEC中涡旋对的研究^[17]

关于获得超冷分子样品研究其长程态光谱特性的实验研究一直是一个比较麻烦的问题，但是我国山西大学在近年来取得了较大的进展和一些研究成果。来自山西大学的科研成员们在经历了一次一次的失败之后，终于成功实现了在外场之中稳定操控分子量子气体形式的RbCs。这个伟大的研究成果标志着我国有关超冷原子的科研水平不仅没有掉队，反而领头羊般地向着研究领域的高峰攀登而去。

而武汉大学研究人员们也不甘示弱，他们为了实现处理光子的有关于自旋方面的信息，把光子SOC运用到纳米尺度的级别，并通过这种巧妙的运用如同通信那般对光子的自由度进行调制亦或是编码。如同下图所示，为了使得光子的轨迹产生所需的弯曲，武汉大学的研究人员们采用在纳米线端头产生SOC的方式以达到效果。武汉大学的这次研究成果对于建设新兴的光学器件体系和系统的制造提供了非常有用的理论依据，也标志着我国光学学器件的设计和理论知识紧跟时代步伐，对于SOC所带来的研究成果也十分的重视。

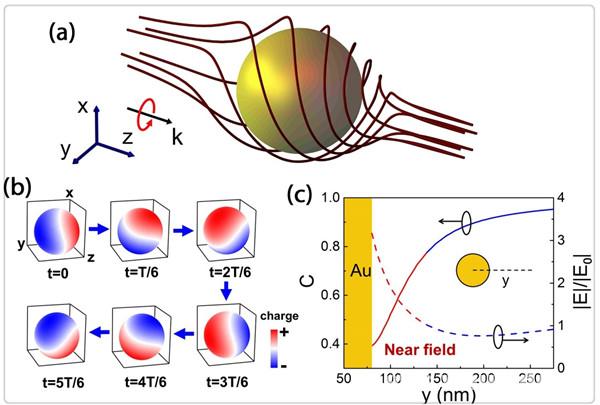
图1.2 金属纳米结构表面等离激元激发过程中光子SOC效应的巨大增强现象^[18]

而最近，来自合肥科学物质研究院的张昌锦在研究有关强SOC的材料的实验中，发现了可以在SOC的这个体系之下通过一系列的处理方式如化学掺杂，高温或者低温等等的方式改变Sr2IrO4这个材料的一些特性。通过张昌锦博士的研究，我们发现了自旋轨道耦合体系中，通过某种处理的方式来控制材料的超导性质的可行性。这为将来在SOC系统里面调控或者是寻找材料的某种特性提供许许多多的经验或者是借鉴。

1.3 本文研究内容

本文主要研究是根据自旋轨道耦合的原理，从理论出发先先了解双拉曼光束的自旋轨道耦合，计算原子在真空中的哈密顿量的能量本征值，通过能量与动量的拟合曲线，改变一些相应的参数（如失谐，耦合强度等），分析真空色散曲线的影响因素。再用一光学腔替换一束拉曼光，用量化的光场模拟腔内冷原子自旋轨道耦合，并通过转化，简化计算其哈密顿量，将其的能级E和动量K进行拟合，改变一些相应的参数，分析腔内色散曲线的影响因素。

具体研究内容包括：

（1）从狄拉克方程出发了解自旋轨道耦合的基本原理，以理论的人造规范场计算系统的哈密顿量，在用实际的双拉曼光束（或光学腔）耦合进行其系统哈密顿量的计算，得到E,K。

（2）用所求得的系统的哈密顿量的能级本征值表达式，通过软件的代码的编写进行E与K的曲线拟合。

（3）根据仿真的曲线模型，改变拉曼失谐以及耦合强度，观察曲线的规律变化，并分析原因。

第2章 自旋轨道耦合的原理

本章着重介绍自旋轨道耦合的基本原理。由于自旋轨道耦合是一种相对论效应，因此，量子力学中的狄拉克方程成为了本章的基础知识。我们从狄拉克方程出发，讨论粒子的哈密顿量以及规范场的知识，讲述粒子的自旋轨道耦合，通过电子的自旋轨道耦合，引出中性原子的自旋轨道耦合。

2.1 狄拉克方程

英国物理学家保罗·狄拉克于1928年建立狄拉克方程，是相对论量子力学的一项描述自旋-½粒子的波函数方程，狄拉克方程可以同时遵守狭义相对论和量子力学的原理，这个方程在实际上是属于薛定谔方程的洛伦兹协变式。并且狄拉克方程曾经预言反粒子是存在的，它的形式为：

其中分别是4阶矩阵，H即为此方程的哈密顿量，是波函数，是光速，是动量。通过解这个狄拉克方程，求它的能量本征值，可以得到其能级E有正和负两个本征值，且彼此相反，理论上充实了狄拉克的预言。在1932年，卡尔·安德森发现了正电子，从而证实了反粒子的存在。

那什么是自旋轨道耦合呢？自旋轨道耦合指：耦合电子的自旋自由度和它的轨道自由度之间的关系，是粒子的自旋与轨道动量的相互作用引起的轨道能级上的细小的分裂。

我们从两个方面解释原理：

1. 从狄拉克方程出发。狄拉克方程有一个十分重要的性质，也就是粒子的自旋是内禀包含在狄拉克方程中的，这说明了在理论上，粒子的自旋角动量和粒子运动的轨道角动量是可以耦合在一起，相互影响的。
2. 从具体的例子出发。我们用电子围绕原子核转动作为一个典型例子。首先我们都知道，原子核带正电，对带负电荷的电子具有库仑力的作用，使它做绕原子核的不规则环形轨道运动。而带负电荷的电子相对于原子核，在运动过程中会产生磁场，反过来从原子核的角度来看，它相对于运动的电子是在旋转的，因而可以说是原子核产生了影响电子运动的磁场。因而电子自身的运动引发的原子核对它的洛伦兹力，再影响电子自身的运动，这就是自旋轨道耦合。

图2.1 电子绕原子核运动

2.2规范场和自旋轨道耦合

粒子和场的相互作用，不仅仅影响粒子的一些特征（如动量，势能，速度甚至质量），也会影响场的一些性质。自旋轨道耦合就属于粒子和场相互影响的其中一种。因此我们在研究自旋轨道耦合之前，需要了解一些相关的“场”的基本性质。

规范势场分为阿贝尔和非阿贝尔两种类型。当场的矢量彼此对易时，这个规范势即为阿贝尔规范势，反之为非阿贝尔规范势。例如磁场就是阿贝尔规范势场。

例如自旋轨道耦合比较经常使用的是非阿贝尔规范势场，在规范势A中，其哈密顿量如下：

2.3 电子的自旋轨道耦合

冷原子是一种中性原子，理论上在电磁场中总体呈电中性，因而不受到库仑力和洛伦兹力。所以在研究冷原子的自旋轨道耦合之前，我们先从电子入手，研究其的自旋轨道耦合的哈密顿量，找到研究冷原子自旋轨道耦合的方法。

对于一个处于电磁场中的运动的电子，他受到库仑力和洛伦兹力，因而具有电场能量和磁场能量，因而它的哈密顿量是：

其中A,分别为电磁的矢势和标势。

因此我们只需要根据相应的参数，求出这个哈密顿量的能量本征值，并且将哈密顿量的能量本征值同电子的动量拟合，就可以观察到电子自旋轨道耦合的色散曲线了。

2.4 原子的自旋轨道耦合

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：