摘 要

光栅被普遍应用于科学研究与社会生产的各个方面，它不仅是人们熟知的分光与色散元件，还可作为成像元件。能够成像的理论支持就是双光栅色散—汇合光谱成像效应，即利用光栅的色散、汇合光谱成像效应的配合，使多波长物光通过第一片光栅的色散作用和第二片光栅的汇合光谱作用后，形成消色散的物体虚像。它独特的色散、汇合光谱成像过程，提供了一种在成像的可能性。本论文基于双光栅色散－汇合光谱成像效应进行了成像研究和全息再现。

在理论基础上推算出双光栅成像方程，并进行实验验证。实验观察可知双光栅衍射所成的像与原物之间存在横纵偏移量，理论分析推理影响横纵偏移量的因素。并将双光栅成像系统中其中一篇光栅换成全息干片，利用双光栅衍射成像的原理，提出了白光—光栅再现全息图的方法并进行实验观察。

双光栅衍射成像作为白光—光栅再现全息图的理论基础，由于只要满足双光栅成像方程的光栅组合，双光栅衍射现象就会发生，所以这个方法具有对光栅频率无特殊要求的优点。

关键词：汇合光谱；双光栅；白光全息再现像

Abstract

Grating is widely used in various aspects of scientific research and social production and life. It is not only a well-known optical and dispersive element, but also an imaging element. The dual grating dispersion-confluence spectral imaging effect is to make use of the combination of the dispersion and confluence spectral imaging effects of the grating skillfully, so that the multi-wavelength object light passes through the dispersion effect of the first grating and the confluence spectral effect of the second grating, and then forms the object image of dispersion elimination. Because of its unique dispersive and confluent spectral imaging process, it provides a possibility in imaging. In this paper, the imaging research is based on the dual grating dispersion-confluence spectral imaging effect.

On this basis, the imaging equation of double gratings is deduced theoretically and verified experimentally. There is a transverse and vertical offset between the image of double grating diffraction and the image of zero-order diffraction of the object passing through the first grating. The factors affecting the transverse and vertical offset are analyzed theoretically. The second grating in the double grating diffraction imaging system is replaced by a hologram. From the point of view of double grating diffraction imaging, a white light-grating reconstructed ordinary transmission hologram is proposed.

Double grating diffraction imaging is the theoretical basis of white light-grating reconstruction hologram. Because of the combination of gratings satisfying the imaging equation of double gratings, the diffraction phenomenon of double gratings will occur, so the white light-grating reconstructed hologram has the advantage of no special requirement for the frequency of gratings.

Key words: Confluence spectrum; Double grating; White-light holographic reconstruction image

目 录

第1章 绪论 1

1.1 研究背景 1

1.2 研究目的及意义 1

1.3 国内外研究现状 2

1.4 课题研究内容及预期目标 2

1.4.1 课题研究的内容 2

1.4.2 研究的预期目标 3

第2章 双光栅成像系统的原理 4

2.1 光栅成像效应概述 4

2.1.1 Talbot效应 4

2.1.2 Lau效应 5

2.1.3 双光栅色散—汇合光谱成像效应 5

2.2 双光栅成像系统的成像方程 7

2.3 双光栅成像系统的实验路线 9

2.4 双光栅成像系统实验结果分析 10

2.4.1 数据分析 10

2.4.2 现象分析 13

第3章 双光栅成像系统成像位置的研究 16

3.1 双光栅成像系统中的虚像位置 16

3.2 横向和纵向偏移量的理论分析 18

第4章 白光再现象的研究 20

4.1 全息白光再现象的理论原理 20

4.2 全息白光再现象的实验路线 24

4.3 白光全息图的再现现象 25

第5章 结论 27

5.1 主要研究成果及结论 27

5.2 研究的意义和作用 27

5.3 还存在的问题及展望 27

参考文献 28

致 谢 29

第1章 绪论

1.1 研究背景

光的衍射现象是光在传播过程中的重要属性之一，是指光波在传播时遇到障碍物，发生偏离直线传播的光学现象。索末菲把“不能用折射或是反射解释的、光线相对直线光路的任何偏离”定义为衍射。首先观察到衍射现象并对其作出精确描述的是格里马尔迪。1678年，惠更斯提出了解释衍射现象的重要原理——惠更斯原理。其主要内容是：光波扰动所到达的每一点都会引起一个次级波源的产生，每一个次级波源所发出的次级球面波向周围扩展，所有次级波的包络面便是新的波前。惠更斯原理主要用来确定波的传播方向，但不能给出光波光强的定量分析^[1]。光的衍射在近现代科学中已经产生了极其重要的作用。

衍射光栅是一种应用很广泛，在学习和科研中都起到很大作用的光学元件。夫琅禾费在1819年用金属丝制成的栅网，是世界上最早的光栅。如今的光栅主要是在平板玻璃或金属板上刻划出刻痕制成的，这些刻痕一般都是等间距等宽。在光栅理论和技术的快速发展之下，如今的光栅衍射单元已不再只是通常意义下的狭缝了，凡是能使入射光的振幅和相位产生周期性空间调制的光学元件，都可以称之为光栅。从这个意义上来说，出现了晶体光栅、超声光栅、晶体折射率光栅等新型光栅^[2]。

光栅可以根据不同的分类标准进行分类。根据光的出射特性可分为透射光栅和反射光栅：具体来说，透射光栅是指在一块透明基体上刻划一系列平行且紧靠的凹槽，而反射式光栅则是在金属反射面上画出一道道刻痕，在刻痕处发生漫反射，在未刻痕处发生反射从而产生衍射现象；根据光栅的作用不同可分为液晶光栅、超声光栅、光纤光栅、计量光栅、耦合光栅、微波光栅、光谱光栅，其中光纤光栅应用比较广泛；根据折射率调制的方式不同可以将光栅分为浮雕光栅和体光栅；根据光栅的槽形可分为锯齿形光栅、矩形光栅、梯形光栅和正弦光栅^[3]。

1960年代以来，衍射光栅作为色散元件，广泛应用于光谱分析，是分析物质成分、探索宇宙奥秘、开发大自然的必用仪器，极大地推动了包括物理学、天文学、化学、生物学等科学的全面发展^[4]。与此同时，光栅的汇合光谱特性得以发现和深入研究。

1.2 研究目的及意义

通过学习了解到光栅的分光特性及光栅的汇合光谱特性，可以由此得到光栅除了色散之外的其他研究方向。通过理论计算得到双光栅成像方程，分析成像条件，就可以做成双光栅成像系统，用来实现“隔屏观物”的现象。在实验过程中还可以分析此光栅成像系统的影响因素，了解双光栅成像的横纵向位移等等。这些研究都可以作为研究双光栅成像仪和双光栅成像实验教学的基础，帮助我们对衍射光栅的各种特性进行更多的了解和学习。

同时还可由此原理，作进一步研究，研究全息相片的白光再现像，将其中一片光栅换成全息干板，调整光路，可以实现全息相片的白光再现像，从另一个角度了解衍射光栅的应用。 这一方法的提出可以摆脱全息图再现时对器械和特殊光学条件的依赖，再现出全息图像，拓宽了全息技术在各个领域的应用^[3]。

1.3 国内外研究现状

光栅的发展过程，是由简单到复杂、由单一刻划到全息光栅的过程。在光栅发展早期，人们对光栅的认识还比较粗浅，在光栅的制作上也刚刚开始起步。从夫琅禾费开始进行，人们对刻划光栅有了更多研究，发现了光栅的色散特性。由此光栅可以作为一种分光元件，用来获得光谱，之后更是广泛应用于信息存储、高功率激光脉冲压缩、光波调制等诸多领域^[5]。

然而，长期以来，传统的光栅衍射研究具有片面性，它引入了光栅的光学分裂和色散，但不包括组合光谱成像效应和双光栅衍射成像效应。这里的光栅汇合光谱特性是指，不同入射角的各色光束经过光栅衍射后，可以得到相同出射角光束的性质，这个特性可以看做是光栅色散性质的逆向理解。所以光栅不仅具有光的分散和分离功能，而且还具有色散光谱的汇聚功能。

如今对光栅的研究不再局限于光栅的色散特性，根据光路可逆原理，我们对光栅的汇合光谱特性进行了研究。2001年，广西大学的张卫平教授首先发表了关于利用双光栅对物体成像的论文，并对这一现象进行了深入的研究。在双光栅对物体成像的基础上，一种基于双光栅对物体成消色散效应的图像传递方法被提出。进而，双光栅的消色散成像原理和消色散成像条件也在2006年被提出来^[13]。在此基础上，我们可以进行双光栅成像系统的具体研究，并由双光栅成像原理发展全息相片白光再现象的实验和研究。

1.4 课题研究内容及预期目标

1.4.1 课题研究的内容

本次课题研究分三步进行：首先是在理论上先掌握光栅的色散和汇合光谱成像效应，了解双光栅系统的成像原理；讨论双光栅组合系统的衍射特性，研究该系统的成像特性和规律，通过理论推算双光栅成像方程。除此之外，根据推算出来的成像方程，我们可以得到双光栅的成像条件，分析双光栅的成效特性研究成像的位置，物像的横纵向偏移等等。同时，提出了白光—光栅再现普通透射全息图的方法，并且通过理论计算分析全息相片白光再现像的可行性和成像条件。

然后开始根据理论分析进行实验验证，利用已学知识和资料，根据推算出的双光栅成像方程，分析双光栅衍射系统的衍射特性，搭建双光栅成像系统的实验装置，观察并验证双光栅成像。采取100线/mm、300线/mm和600线/mm几种不同组合的光栅进行实际研究，通过测量实验数据对比分析，了解双光栅成像的可行性，证明双光栅衍射成像方程的正确性。同时讨论影响双光栅系统成像的各个因素，分析成像条件与物像偏移； 在双光栅成像实验中改变光栅空间频率或双光栅到物体的距离，测量实验数据，对比理论数据，对影响成像的因素做深入研究讨论。实验中对物像偏移进行分析，了解双光栅成像系统在成像过程中发生的偏移情况。

将双光栅成像系统中的其中一片光栅换成全息相片，透过全息相片观察在白光光源的照射下全息相片的再现现象，观察全息相片白光再现像的成像特性。这是光栅汇合光谱特性的另一重要应用。

最后，对实验现象和数据进行整理和分析，对理论研究，验证理论的正确性。了解双光栅成像系统的成像现象和成像特性，全息相片白光再现像的现象和特性，记录在报告里，作为这一次研究的成果。

1.4.2 研究的预期目标

通过理论分析掌握衍射光栅新的特性，了解双光栅成像系统的具体原理，搭建双光栅成像实验装置，通过实验验证双光栅系统的成像方程，分析各个影响因素对成像的影响，在此基础上得到物像的横纵向位移的变化。通过双光栅成像系统的研究，了解光栅的汇合光谱特性，同时利用这个特性，掌握全息相片的白光再现像的原理并实验验证分析。

第2章 双光栅成像系统的原理

2.1 光栅成像效应概述

光栅作为一种传统的重要光学元件，一直在科研、生产、生活中扮演着重要的角色。光栅的分光功能与色散作用一直为人们所熟知并被广泛应用于光谱成像和光谱分析领域。光栅还有成像的作用，被人们所熟知的光栅成像效应有Talbot效应、Lau效应以及双光栅色散－汇合光谱成像效应等^[13]。这里对光栅的成像效应做一个概述。

2.1.1 Talbot效应

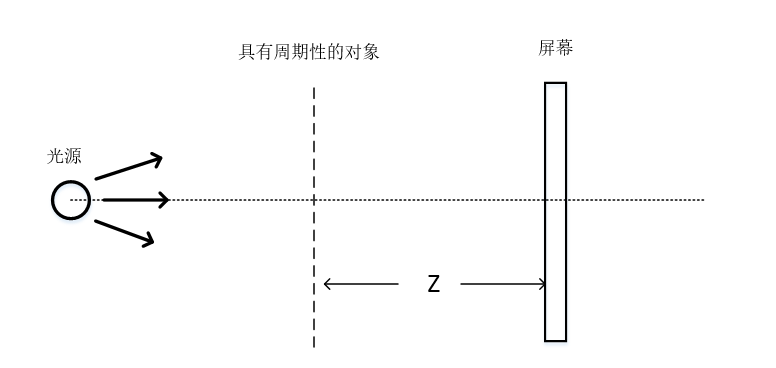
图2.1 Talbot效应示意图

Talbot效应指的是单色平面波垂直照射在一个具有周期性透射率画数的物体（如等周期光栅）时，在该物体后的某些距离会出现该周期函数的物体的像。这个像到物体的距离Ｚ为

（2.1）

上式中的d为光栅常数，lambda;为入射光单色波波长，m=1,2,3hellip;hellip;。

Talbot效应是Talbot在1836年发现的，目前人们己经用衍射干渉等多种理论进行了分析解释，也将Talbot效应扩展到了广义的Talbot效应。人们对Talbot效应的应用也进行了广泛的研究，己经将这一效应应用于准直测量、图像分解、角度测量、光谱测定、折射测量、透射焦距测量等^[13]。

Talbot效应的成像物体要求是具有周期性结构的物体，因此在使用光栅进行Talbot效应成像时，所成的像实际上是光栅自身的像，而不能对具有非周期性结构的物体成像^[13]。

2.1.2 Lau效应

Lau效应指的是用扩展光源照明两个周期一样、相隔一定距离的衍射光栅，就可以在无穷远处得到平面干涉条纹的现象，这一现象是Lau在1948年首先发现的^[13]。

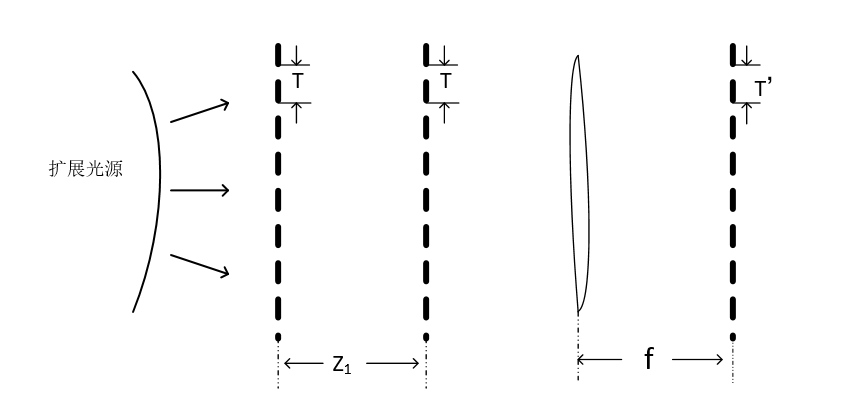
图2.2 Lau效应示意图

图2.2为Lau效应的成像示意图，图中第一片光栅和第二光栅的周期都为T，透镜的焦距为f，两片光栅的距离为。用波长为lambda;的非相干光照明衍射光栅时，在满足下式时：

（2.2）

alpha;，beta;为整数，所成的干涉条纹的周期可以表示为：

（2.3）

Lau效应所成的平行干涉条纹可以认为是第二片光栅对第一片光栅所成的像，只能对具有周期性结构的物体进行成像，无法对不具有周期性结构的物体成像，成像位置在无穷远处。目前Lau效应也被广泛应用于众多领域，如测量透镜焦距、测量位移、图像合成、测光束准直、测量波长、光学编码等^[13]。

2.1.3 双光栅色散—汇合光谱成像效应

双光栅色散—汇合光谱成像效应是指物光波经过两光栅的两次衍射后仍能形成物体虚像的效应，其中第一片光栅的作用是色散，第二片光栅的作用是汇合光谱，光栅的逆效应（即汇合光谱作用）将被第一片光栅色散开的多波长物光再次汇合成一束，形成消色散的物体像^[13]。是与Talbot效应和Lau效应完全不同的。

双光栅成像是利用光栅的色散和汇合光谱特性来实现的。第一片光栅将多波长光的物光波色散，形成物光谱；第二片光栅利用光栅的汇合光谱特性，将第一片光栅产生的物光谱汇合形成消色散的原物体图像。这就是双光栅色散－汇合光谱效应形成消色散像的原理。

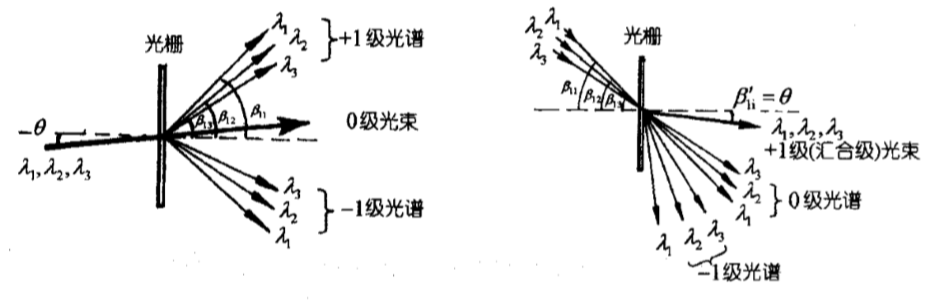
图2.3 多波长光束通过光栅示意图

2.3左图表示三色混合光束通过光栅被衍射形成分散光谱，2.3右图边表示三色分光束以不同角度进入光栅被衍射，其中 1级为汇合光束。

利用光栅的汇合光谱特性，可将由于光栅衍分散的光束汇合起来，重新汇聚形成清晰的图像。如果让某一物体发出的光束经过光栅被衍射形成色散光谱后，使其中某一级光谱进入另一光栅并满足光谱汇合条件，则通过另一光栅衍射后的汇合光束可以看到该物体的图像。因此，将两片光栅以一定的条件组合起来可以形成图像传递系统—双光栅成像系统。

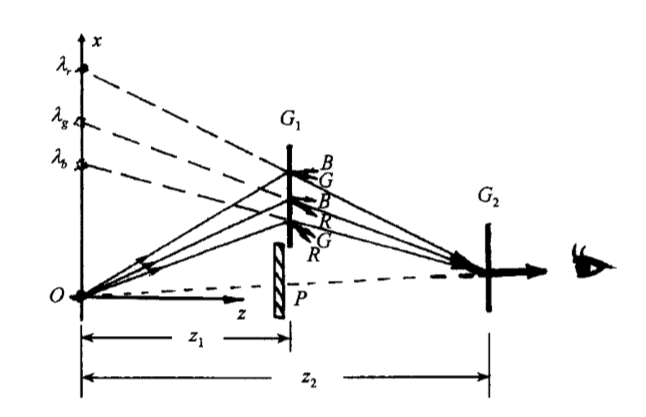如图2.4所示，G₁和G₂为两片平行的透射光栅，O为观察目标物，P为挡板。光栅G₁可以使来自于物体O的光衍射为各级物光谱，因为要求衍射产生的一级衍射光亮度高、质量好，保持最终得到失真最小的成像，光栅G₁需要置于能使一级衍射光处于最小偏向角的位置。而光栅G₂放在一级衍射光束的路径的适当位置。

图2.4 双光栅衍射成像光路图