角向偏振拉盖尔-高斯光束的紧聚焦特性毕业论文
2020-02-23 21:54:30
摘 要
拉盖尔-高斯光束是一种特殊的矢量光束,它是一种非均匀偏振光,具有圆柱对称形式。
该光束进过高数值孔径透镜进行紧聚焦后会产生一些特殊的聚焦光场,这种聚焦可以广泛应用于高粒子导引或陷波, 扫描光学显微镜,光刻,金属激光切割,粒子加速等方面。因此近年来越来越多的学者将目光放在了这个方面。
在本论文中,主要研究拉盖尔-高斯光束紧聚焦后的特性,分析焦点附近的光场强度分布,对比各种光束间的不同特性,以此来探究聚焦特性在各个领域的应用前景。
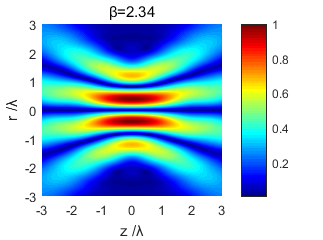
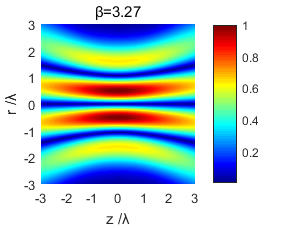
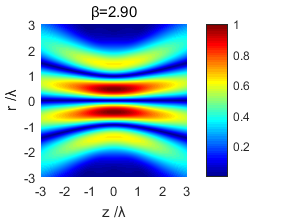
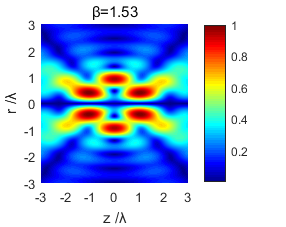
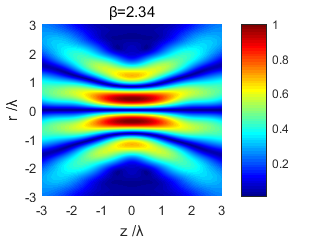
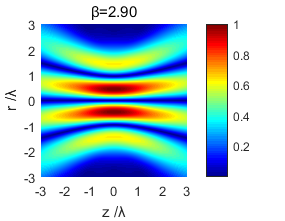
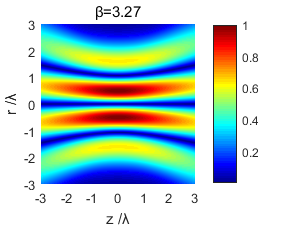
使用MATLAB仿真软件对紧聚焦后的光场分布进行了模拟仿真,得到了不同截断参数下的光场分布图样,通过对不同条件下光场分布图的研究对比,得出了光场分布和截断参数的变化关系,分析出紧聚焦特性。
关键词:拉盖尔-高斯光束;聚焦特性;角向偏振
Abstract
The Laguerre-Gaussian beam is a special vector beam, which is a non-uniformly polarized beam and has a cylindrically symmetrical form. After the beam enters the high numerical aperture lens, it will produce some special focused light fields. This focus can be widely used in high particle guidance or notch, scanning optical microscope, lithography, metal laser cutting, particle acceleration, etc. aspect. Therefore, more and more scholars have set their sights on this aspect in recent years.
In this dissertation, we mainly study the characteristics of Laguerre-Gaussian beams after they are tightly focused, analyze the intensity distribution of the optical field near the focal point, and compare the different characteristics of the various beams to explore the application prospects of focusing characteristics in various fields.
Using MATLAB simulation software to simulate the light field distribution after tight focusing, the light field distribution patterns under different truncation parameters were obtained. By comparing and studying the light field distribution map under different conditions, the light field distribution and truncation were obtained. The relationship between the parameters changes and the tight focus characteristics are analyzed.
Key Words: Laguerre-Gaussian beam; Focusing characteristics; Angular polarization
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1 拉盖尔-高斯光束(Laguerre-Gaussian beam)简单介绍 1
1.2拉盖尔-高斯光束(Laguerre-Gaussian beam)的研究历史及现状 2
1.3拉盖尔-高斯光束(Laguerre-Gaussian beam)的产生方法 3
1.4 研究目标及内容安排 3
第2章 拉盖尔-高斯光束的聚焦模型 5
2.1 基本理论 5
2.1.1拉盖尔-高斯光束的偏振态 5
2.1.2 切趾函数 6
2.1.3 Richards-Wolf矢量衍射理论 7
2.1.4 光强分布公式推导 8
2.2.MATLAB模拟 10
2.3 本章小结 12
第3章 拉盖尔-高斯光束紧聚焦分析 13
3.1 光场分析 13
3.2 本章小结 15
第4章 结论和展望 17
4.1 工作总结 17
4.2 展望 17
参考文献 19
致 谢 20
第1章 绪论
1.1 拉盖尔-高斯光束(Laguerre-Gaussian beam)简单介绍
我们每天都能见到光,这么多年来对光的研究一直没有间断过,科学家们发现了各种光的重要性质并逐渐将这些性质转化为可应用于生活研究中的各种器件。这些性质中,光的偏振一直是科学家研究的热点以及前沿。偏振光可广泛应用于数据储存、激光钻孔、光通信、机械加工和生物医学成像等应用中。本文主要研究角向偏振的拉盖尔-高斯光束(Laguerre-Gaussian beam),后文用LGB表示。光矢量的振动方向具有某一种特定规则变化或者不发生变化的光束叫做偏振光。而偏振光又分为均匀偏振光(uniformly polarized light)[1-3]以及非均匀偏振光(Non-uniformly polarized light),常见的均匀偏振光有椭圆偏振光,平面偏振光,部分偏振光等。均匀偏振光的偏振态相对来说要比非均匀偏振光简单,非均匀偏振光随着空间分布发生变化它的的偏振状态在光束的横截面上随之变化是其主要特点。同时,科学家们在过去的科学研究中也更加关注在空间有均匀分布的偏振光,但是,近些年由于发现了许多非均匀偏振光独特的性质和潜在的应用价值,非均匀的偏振光吸引了越来越多的人的兴趣。
LGB就是典型的非均匀偏振光,它是其中的特例,因为LGB的偏振是圆柱对称的,所以又是圆柱矢量光束的一种,本文主要研究其角向分量。越来越多科学家关注激光光束,因其经过大数值孔径聚焦系统的聚焦后,其性质具有特殊性和潜在应用具有重要性。研究结果表明,当激光光束强聚焦后,在焦点附近会产生一个纵向分量,这个分量的强度十分大,并且产生的光斑比普通聚焦光斑也要小得多,这种聚焦可以广泛应用于高粒子导引或陷波, 扫描光学显微镜,光刻,金属激光切割,粒子加速等方面。本文重点研究角向偏振拉盖尔-高斯光束经过大数值孔径聚焦系统的聚焦特性。
根据传统的傍轴衍射理论,可以解释大部分传统光学器件的光学现象,如基尔霍夫衍射理论(Kirchhoff diffraction theory)[4-5]和瑞利—索末菲标量衍射理论(Rayleigh-Sommerfeld scalar diffraction theory)[6]都能准确描绘衍射光场的特性。然而高数值孔径的透镜聚焦效果极强,入射光束经过透镜后光线传播方向急剧改变,即紧聚焦,此时,分析光的传播以及光场就不能使用惠更斯菲涅尔(Huygens-Freyner)原理了,会产生较大误差。当透镜的数值孔径比较小时,光线的传播满足广义的折射定律,光线的变迹(即切趾)和像差等效应对光线传播影响很小,可以忽略不计。当透镜的数值孔径大时这些效应就不能忽略,就应该加以考虑了。此时,我们可以用Richards-Wolf 模型所给出的矢量衍射理论给出焦点附近的光束特性。
因此,以拉盖尔-高斯光束为研究对象,具体研究角向偏振拉盖尔-高斯光束在紧聚焦条件下的光束特性显得尤为重要。
1.2 拉盖尔-高斯光束(Laguerre-Gaussian beam)的研究历史及现状
1952年,G.Francia在光学成像系统中加入光瞳滤波器,第一次突破了瑞利衍射极限[7]。
1959 年 B. Richards 和 E. Wolf 提出了理查德沃尔夫(Richards-Wolf )模型,这是一种描述光束经过高数值孔径透镜聚焦之后,在焦点附近光场分布的模型。这个模型是严格的矢量衍射理论在一定条件下近似得到的结果,适合描述距离出射光瞳的距离远远大于波长处的光场分布情况[8]。
1995年王喜庆发现,当光阑大小为正无穷时,可以通过Collins公式将拉盖尔-高斯光束聚焦后的腰斑位置及半径计算出来,且在光阑孔径有限的情况下,对不同模的拉盖尔-高斯光束其值进行了数值计算[9]。
2000年K.S.Youngworth利用Richards-Wolf理论对柱对称矢量光束进行了研究,对其聚焦特性进行了分析并计算了焦点附近光场分布。研究发现角向偏振拉盖尔-高斯光束经聚焦后呈中空型的分布。
2004年,C.J.R.Sheppard及其他学者在研究径向偏振光束时发现其可以提升显微镜的分辨率。
2008 年,H. F. Wang, L. P. Shi, B. Lukyanchuk, C. Sheppard 和C. T. Chong发现入射光的偏振状态可以通过将光入射到衍射光学器件( diffractiveoptical elements,DOE)中来改变,出射后的光焦点附近的光场分布情况会发生改变[10]。
2010年,K.B. Rajesh等人对双环形偏振光束进行了研究,将该光束通过高数值孔径的轴锥透镜后,研究其聚焦性质。在此基础上提出了一种用于产生纵向极化光束的子波长(0.45微米)的方法,该光束在约8英里的空间长度上无扩散地传播。这是通过紧聚焦来实现的。这是通过用高NA透镜轴棱锥的紧聚焦来实现的,它利用球面像差复制轴棱镜的性能并产生扩展焦线。基于矢量衍射理论计算了光强分布,发现在高数值孔径(Na)透镜轴棱镜的情况下,焦点附近的总光强分布对入射光的截断程度影响不大。
2011年,B.Tian及其他学者从理论上对双环形角向偏振光束进行了去研究,将光束经过高NA物镜聚焦后,在焦点附近得到长聚焦深度的亚波长焦洞。这些无衍射的暗通道在原子开关、原子透镜、原子光学实验这些方面的应用上有很大潜力。
2013年,顾敏等人在K.S.Youngworth利用Richards-Wolf理论研究矢量光束聚焦的基础上,通过聚焦三种不同的涡旋光束(角向偏振、径向偏振、圆偏振),通过三者的比较发现,角向偏振漩涡光束可得到纯的纵向磁斑[11]。
2014年,S.Wang等人发现,使用涡旋相位滤波器将角向偏振光束调制后,可产生亚波长的纵向磁针,产生的磁针能够用来捕获原子。
2015年,田博,蒲继雄等人将角向偏振高阶拉盖尔-高斯光束(Laguerre-Gaussian beam)经过高数值孔径透镜和衍射光学元件( diffractiveoptical elements,DOE) 组成的光学系统,使用德拜矢量积分计算光场分布,研究焦点附近的紧聚焦特性。研究发现,入射光束通过衍射光学器件( diffractiveoptical elements,DOE)整形以后,在焦平面附近产生会光链,光链的数目和特性都可以通过衍射光学器件进行控制。因此光链可以灵活运用到各个领域里[12]。
1.3 拉盖尔-高斯光束(Laguerre-Gaussian beam)的产生方法
想要研究拉盖尔-高斯光束,首先需要产生拉盖尔-高斯光束,下面简要介绍一下该光束的产生方法。
现阶段主要使用空间光调制器产生拉盖尔-高斯光束[13]。空间光调制器是一种功能强大的光电器件,能够改变光的基本性质:振幅,相位,偏振。其中振幅通过改变光场调制,相位通过改变折射率调制,偏振通过旋转偏振面调制。不仅如此,空间光调制器还能将非相干光转化为相干光。
产生拉盖尔-高斯光束,首先要计算出光束在z=0处的相位、振幅等的表达式。空间光调制器里有许多可被电信号控制的小单元,经过这些单元的光的基本性质受电信号的控制,并随电信号的改变而改变。因此空间光调制器可以通过电信号对每个像素的光束进行精准的调制,此时就可根据光束的特征表达式计算出来的结果进行精准的调制。也就是说只要将表达了所需要光束各个基本性质的表达式求出来,就可以使用空间光调制器产生所需要的光束。
除了使用空间光调制器外,拉盖尔-高斯光束也可以使用相位片角向衍射产生。众所周知,LG光束是一种涡旋光束,具有螺旋波阵面。因此使用标准的基模高斯光束经过一个具有螺旋形的相位片后,高斯光束便具有了螺旋波阵面变成拉盖尔-高斯光束。但是相位片的制作工艺比较复杂,需要进行精确的刻蚀等操作,制作相位片的原料也是特殊的玻璃片,成本较高。刻蚀过程中需要用到各种精密仪器,精准的材料用量。所以该方法一般只用于实验研究,并不能大范围适用。
1.4 研究目标及内容安排
针对目前学者对拉盖尔-高斯光束(Laguerre-Gaussian beam)的研究现状,论文确立了以下研究目标:
1)分析角向偏振拉盖尔-高斯光束基本概念以及应用前景。简要介绍拉盖尔-高斯光束的产生方法。
2)运用B.Richards 和 E.Wolf 提出的矢量衍射理论,计算焦点附近光场分布。数值分析角向偏振拉盖尔-高斯光束(Laguerre-Gaussian beam)聚焦系统的基本原理,建立角向偏振拉盖尔-高斯光束的聚焦模型,探讨其潜在应用,同时对径向偏振LG光束以及LBG光束的聚焦原理进行简单对比分析。
3)以聚焦光场的计算结果为基础,分析角向偏振拉盖尔-高斯光束的紧聚焦特性。并与径向偏振拉盖尔-高斯光束以及径向偏振拉盖尔-贝塞尔-高斯光束的紧聚焦特性进行比较。对比各种光束紧聚焦后的性质,分析它们的不同之处以及潜在应用。
结合以上的研究目标,本人对论文研究内容作了如下安排:
第1章,绪论。介绍了拉盖尔-高斯光束的基本概念、研究历史以及现状,确定论文的研究目标及内容安排。
第2章,建立角向偏振拉盖尔-高斯光束的聚焦模型,基于B Richards 和 E Wolf 提出的矢量衍射理论,推导了拉盖尔-高斯光束在自由空间中的聚焦场的数学表达式。
第3章,使用MATLAB模拟所建立的聚焦场,数值分析了拉盖尔-高斯光束聚焦系统的基本原理和聚焦场强度分布特性。对比其他圆柱矢量光束紧聚焦的特性。
第4章,结论和展望。总结拉盖尔-高斯光束的紧聚焦内容,并在此基础上提出一些本人做得不够完善的地方以及提出一些值得对其进一步研究分析的问题。
第2章 拉盖尔-高斯光束的聚焦模型
在前面第一章已经有所介绍,矢量光束相较于标量光束有很多特殊的性质,拉盖尔-高斯光束的聚焦特性与普通标量光束的聚焦特性相比有很多特殊之处,并且在医学,生物,物理等领域内这些特殊的性质都有被利用到,因为矢量光束的聚焦特性的研究非常具有应用潜力。这些年来,许多学者对矢量光束的聚焦特性作了更加深入的研究:Lu Wang等人研究了紧聚焦角向偏振涡旋光束的磁化场特性 ,Bo Tian等人研究了角向偏振高阶拉盖尔高斯光束强聚焦产生双光链,Hong Zhang等人研究了紧聚焦圆柱矢量光束捕获多个粒子 。本章主要基于B Richards 和 E Wolf 提出的矢量衍射理论,在他们讨论过的经高数值孔径聚焦的标量光束的聚焦特性的基础上推导拉盖尔-高斯光束[14]在高数值孔径聚焦系统的聚焦场分布的数学表达式,通过数值分析角向偏振拉盖尔-高斯光束的聚焦特性,并与径向偏振的LG以及LBG光束紧聚焦作简单对比。
2.1 基本理论
接下来将简要介绍矢量光束的特殊偏振态、拉盖尔-高斯光束紧聚焦光场分布数学表达式的推导、使用MATLAB模拟紧聚焦光场以及对切趾函数和矢量衍射理论进行简单介绍。
2.1.1 拉盖尔-高斯光束的偏振态
类似于一个普通的矢量可以分解为横向分量和纵向分量,广义的矢量光束也可以进行分解,它能够被分解为径向成分和角向成分[15]。
(a) (b) (c)
图2.1 偏振模式图
上图(a)为广义的矢量光束,图(b)为径向偏振模式,图(c)为角向偏振模式[15]。从图形中可以比较直观的看出来,径向模式就是偏振方向从中心沿着半径指向圆外,角向模式就是偏振方向沿着圆的切角。对于这两种偏振态的定义为,如果场中的每个点的电场矢量相对矢径方向的旋转角度为φ ,则该点的电场强度一般表示为,其中r为径向的单位矢量,θ是角向(切向)的单位矢量,当 φ= 0时,表示径向偏振矢量,当 φ≠ 0时,为角向偏振矢量[20]。本文主要研究角向偏振模式。
2.1.2 切趾函数
在计算光束紧聚焦后焦点附近的光强分布时,由于是使用高数值孔径的物镜聚焦,不能忽略光线的像差以及切趾,因此我们需要用到一个重要的计算工具,那就是切趾函数。下面简单介绍一下切趾函数。
f
M
L(θ)
L(r)
y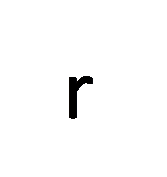
θ
x
r
z
图2.2 高NA聚焦系统几何示意图
上图为高NA聚焦系统几何示意图,光束经高NA物镜M聚焦后形成球面波,最后聚焦在XOY平面上。上图中,透镜的光瞳函数用L(r)表示,经过物镜聚焦后的光场分布可以表示为一个关于汇聚角θ的函数,用L(θ)来表示,这里的L(θ)就是接下来所要介绍的切趾函数。
光瞳函数和切趾函数是用来描述透镜成像原理的重要工具,其中光瞳函数描述光束在被透镜聚焦前横向光场强度分布情况,切趾函数用来描述光束经物镜聚焦后焦点平面与聚焦球面之间的光场强度分布情况,二者略有不同。正如本节开头时所述,只有透镜的数值孔径较大时我们才不会忽略光线的切趾,因为在数值孔径较小时,光瞳函数和切趾函数之间的差别小到可以忽略不计,此时透镜聚焦前后的光线密度分布也是高度相似的。然而在本论文的研究条件下二者之间的差别不能忽视,否则将会导致极大的误差而不能得到正确的光场分布数学表达式。
如图1所示,假设入射光为半径为r的光线,半径r与焦距f满足以下关系:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: