摘 要

异常值检测是进行数据处理和分析之前所必需的预处理操作，对异常值的处理是否得当关系到后面数据分析实验的精确度和数据信息的完整性，因此，研究异常值检测是一个重要的课题。本文通过实验说明了(K)PCA相对一般异常值检测的优势，并且把KPCA应用在高维数据中，构建了主动形状模型，探究不同参数对人脸识别参数的影响。

论文研究了(K)PCA的判异相对优势，以及KPCA在特殊的场景（非线性可分数据）下分类的优良性。在应用方面，我们使用PCA和不同内核KPCA来构建主动形状模型，分别观察不同参数的选取对人脸模型的影响。

研究表明，在判异时，(K)PCA相对传统的判异方法在检测率和误报率都有显著的优势。在采用不同形式的算法进行应用时，不同的算法以及同种算法不同的参数选取都会对分类效果和人脸模型造成影响，我们对此做了可视化处理和直观解释，并结合了(K)PCA做分类的算法和做异常值检测的方法做了论证说明。

本文的特色在于，由(K)PCA做异常值检测作为引入点，同时与(K)PCA做分类的思路结合起来，进行了基于(K)PCA的分类实验，并说明了(K)PCA算法进行样本点分类和进行异常值检测的内在联系。

关键词：（核）主成分分析；异常值检测；人脸识别；样本点分类

Abstract

Outlier detection is a necessary preprocessing operation before data processing and analysis. Correct handling of outliers is related to the accuracy of data analysis experiments and the integrity of data information. Therefore, it is important to study outlier detection. Question. This paper illustrates the advantages of (K)PCA over normal outlier detection, and applies KPCA to high-dimensional data to construct an active shape model to explore the influence of different parameters on face recognition parameters. The main contents and results are divided into the following aspects.

The dissertation studies the comparative advantage of (K)PCA's discriminant and the superiority of KPCA's classification under special scenarios (non-linear separable data). In terms of applications, we use PCA and different kernels KPCA to construct an active shape model, and observe the influence of the selection of different parameters on the face model.

Studies have shown that (K)PCA has a significant advantage over traditional discriminatory methods in terms of detection rate and false alarm rate when discriminating. When using different forms of algorithms to apply, different algorithms and different parameters of the same algorithm will affect the classification effect and face model. We have done a visual processing and intuitive interpretation, and combined with (K)PCA The classification algorithm and the method of doing outlier detection were demonstrated.

The feature of this paper is that (K)PCA does the outlier detection as the introduction point, and at the same time combines the idea of ​​(K)PCA as the classification, performs the classification experiment based on (K)PCA, and explains the (K)PCA algorithm. Intrinsic links for sample point classification and outlier detection.

Key words: （K）PCA；Abnormal value detection；Face recognition；Sample

point classification

目 录

第1章 绪论 1

1.1引言 1

1.2 课题研究的背景和意义 1

1.3 国内外研究现状 2

1.3.1 国内研究现状 2

1.3.2 国外研究现状 2

1.4 研究思路、内容及创新点 3

1.4.1研究思路 3

1.4.2 主要内容 4

1.4.3 创新点 5

第2章 异常值检测的方法 6

2.1 传统异常值检测的方法 6

2.1.1 局部距离法 6

2.1.2 Tukey法 8

2.1.3 三倍偏差法 8

2.2 PCA做异常值检测的方法 8

2.2.1 PCA的算法原理 8

2.2.2 PCA做异常值检测的思路 9

2.3 KPCA做异常值检测的方法 10

2.3.1 KPCA的算法原理 10

2.3.2 KPCA做异常值检测的思路 12

第3章 （K）PCA和判异传统算法的效率比较 13

3.1 实验背景概述 13

3.2 实验数据的采集和预处理 13

3.3 实验的基本思想 14

3.4 实验过程的实现 14

3.5 实验结果和讨论 15

第4章 PCA和KPCA在高维数据下的分类性能差异 16

4.1 异常值检测和样本点分类的关系 16

4.2 基于PCA和KPCA的样本点分类实验 16

4.2.1 数据描述 16

4.2.2 主成分分析法和核主成分分析法 17

第5章 基于KPCA的异常值检测的主动形状模型 19

5.1 研究背景概述 19

5.2 数据描述 19

5.3 实验过程 20

5.3.1重建前置图像 20

5.3.2 高斯核心的原象 20

第6章 展望和总结 23

6.1 参数选择 23

6.2 核主成分分析的直观解释 23

6.3 总结、结论和建议 24

参考文献 25

致谢 26

第1章 绪论

1.1引言

长期以来，异常值的检测在数据分析的预处理中占据有重要的地位，检测异常值的方法也层出不穷，而每种检测异常值的算法的判别优度和效率并没有很明确的比较，人们对这些算法的应用场景也不是很明确，这对我们理解和应用算法必定造成一定的影响。为了明确各种算法的异常值检测的效率和优势，探究它们的应用场景，本文进行了一系列实验，比较了常见的异常值检测的算法在不同数据场景的实际效果，并且基于效果较好的PCA和KPCA算法深入讨论了他们的差异，找到了他们的最佳应用场景，并且基于KPCA做了在高维数据下的异常值检测应用实验。

1.2 课题研究的背景和意义

当我们进行数据分析时，个别数据经常偏离预期值或其他大部分数据，如果对这些数据处理不当，我们可能会造成较大的误差或者遗漏关键信息。这就使得判断出异常值十分重要。目前常用的判异方法还不是十分完善，因此，我们需要进一步研究。

使用PCA来进行异常值检测是有效的一种方法，但它本身有着局限性。它侧重找到维数比原始特征空间更低的子空间，而这样的子空间通常是线性的。实验结果表明，在线性数据下它十分有效，但是当面对高维度数据空间时它显得力不从心。因此，研究它的改进形式的KPCA法来进行异常值检测和处理就具有特别的意义了。

首先它的理论意义在于，在处理实验数据时，如果出现了复杂度较大的数据集，且需要们对异常值进行检测的时候，如果纯粹使用传统的方法来进行我们的实验，也许得到的结果跟我们实际情况有着较大的出入，这时候需要们对算法本身进行一定的探究和改进，因此，在这样的基础下，我们进行这样的实验，通过实验结果来比较传统的算法和(K)PCA在异常值检测的判别率和错误率，从而可以更好的改进算法结构提高数据处理的精度。

其次它的实践意义在于，实验数据处理之后，我们可以根据经过初步处理的数据进行更深层的数据挖掘工作。如果数据异常值没有被消除或者检测出来，不仅会影响数据的精准度，还可能对由此进行的数据分析结果产生影响。由洛伦兹试验的蝴蝶效应我们知道这样的影响可能会是巨大的。因此，进行数据的异常值检测和研究，深入研究其算法和优化算法，不仅对数据本身的完善和清洗十分重要，对未来的数据分析工作的意义也是十分重大的。因此，我们在PCA进行异常值检测和研究的基础上进一步优化，使用KPCA来继续我们的实验和研究。

1.3 国内外研究现状

异常值的检测和研究从数据科学诞生就是研究的热点，数据时代越来越近，数据量的需求和供给都变得十分庞大，而数据清洗正好是数据分析的基础工作，异常值检测在数据清洗中又是重要的一环。由于环境的不同以及各自研究的侧重点存在差异，国内外关于异常值检测的研究和基于(K)PCA的研究存在一些异同。

1.3.1 国内研究现状

国内应用方面主要集中在具体的项目和工程中使用特定的算法进行异常检测。比如刘凤魁、邓春宇(2017)基于电力中大数据的特点去针对性的研究了其异常检测算法，并且使用某省电变压器的数据验证了他们的算法的合理性^[1]。同样的还有在纪素娟(2009)介绍了基于PCA做异常值检测的方法，并和其他的常见判异方法进行比较，说明了该方法的优良性^[2]。 苏卫星、朱云龙(2012)等为了满足工业中过程控制的要求设计的算法，在仿真建模中也得到了很好的应用^[3]。还有方海泉、薛惠锋(2017)把中位数的方法和集成经验模块分解的方法结合了起来，用以检测异常值。他们的做法是先用中位数的方法先把显著的异常点给排除掉，接着使用后面的方法，对剩下来的数据分解，通过叠加低频分量的方法拟合剩下的大多数数据的整体变化趋势，再使用偏差比例来检测异常值^[4]。何奇峰(2006)在时间和空间的两个角度对异常值的检测进行了研究，同时，把这两个方向的内容和异常值检测的结果结合了起来，得到了一种全新的检验时空异常值的方法^[5]。赵新斌(2017)把四分位法和目前在航空界常用的标准差法结合了起来，通过多种维度和方向进行论证，最后证明了四分位法相比标准差法更有优势，更适合应用在航空安全检测上^[6]。刘首华(2016)结合Grubbs、局地异常值检测和波高观测误差控制等三种方法建立了一种新的异常值检测的方法，并进行了实验。实验证明，该方法能够有效的降低判错率^[7]。邓森林(2015)利用一类支持向量机理论，把金融交易数据进行无监督分类，识别交易数据中的可以数据，并且使用仿真数据检验了该算法的有效性^[8]。

1.3.2 国外研究现状

国外方面致力于通过算法模拟运行和理论论述方面比较算法的优良性。 Xiao. Zhang(2017)提出了一种新颖的KPCA方法，用统计平方预测误差的方式来搜索飞行数据集中的异常值，并通过GPU的内核模拟方法来优化置信度，并在GTX660的GPU下实现了较CPU执行速度的112.9倍的速度^[9]。Adathakula Sree Deepthi(2014)论述了异常数据常常是不符合预期的数据或者有明显错误的数据集，往往可以在银行、金融市场、网络场景中存在，并且他们还在文献中论述了各种异常值检测技术以及各自的优缺点^[10]。Fouzi Harrou(2015)把常用的主成分分析法进行了改进，提高了它的判异准确度，降低了判错率，并且基于这个改进的判异方法和急诊室的数据进行了实验拟合，得到了理想的结果^[11]。Kenneth Heafield(2006)使用了改进的PCA方法进行了异常值检测，并且把它应用在网络异常检测上，他同时比较了几种算法的优良性，得出了基于大量数据的较为完整的结论^[12]。Alan J. Izenman(2007)比较了不同核的异常值检测的算法的应用场景，并且基于最小核主成分法进行了一系列的应用^[13]。

1.4 研究思路、内容及创新点

1.4.1研究思路

在这篇论文中，我们先是说明了异常值检测在数据处理和分析中的重要性，让我们对进行异常值检测的必要性有了十分深刻的见解。接着，我们通过查阅资料和文献，熟悉了现在常用的检测异常值一般方法。我们发现，在现在通用的异常数值检测方法中，周围数值点的密度、聚类等方法被经常使用，而一个比较新颖而有效的方法是通过PCA来进行异常值检测的。我们仔细阅读了利用PCA法做异常值检测的文献，发现了它较之一般异常值检测方法具有一定的优势（如检测率较高误报率较低等），因此我们对PCA法进行了更深层次的研究。我们通过实验又发现PCA算法在面临线性不可分的数据的时候，它进行异常数值检测会出现检测率和误报率都不是很理想的情况。因此，我们就需要进行探究，在非线性可分的时候，我们能否把主PCA的优势保留下来，而同时改进它的不足之处。因此，我们就有了基于PCA的算法——KPCA。我们通过实验来观察了KPCA的应用场景和效率，得到了令人满意的效果。最后，我们把KPCA和PCA用于判异的思想和用于分类的思想结合起来进行了一系列实验，说明了KPCA在高维场景下分类的优势，并且它的内核也会影响到他们做异常值检测的效率。最后我们使用KPCA来进行了主动形状模型的构建，并且对参数选择进行了讨论，对高斯核心的KPCA的实验结果进行了解释。

1.4.2 主要内容

第一章，绪论。 在这一章中，我们先是提出了论文的引言，说明了本文的研究方向，并且说明了本文的研究背景以及意义，接着总结了国内外对于这个课题的研究现状，最后确定了本文的研究主要内容、技术路线以及自身的创新点。

第二章，异常值检测的方法。在这一章中，我们先是介绍了三种传统的异常值检测的方法，并且从算法方面介绍了这三种方法的原理。接着我们分别介绍了PCA和KPCA算法的基本原理，以及PCA和KPCA做异常值检测的基本思路。

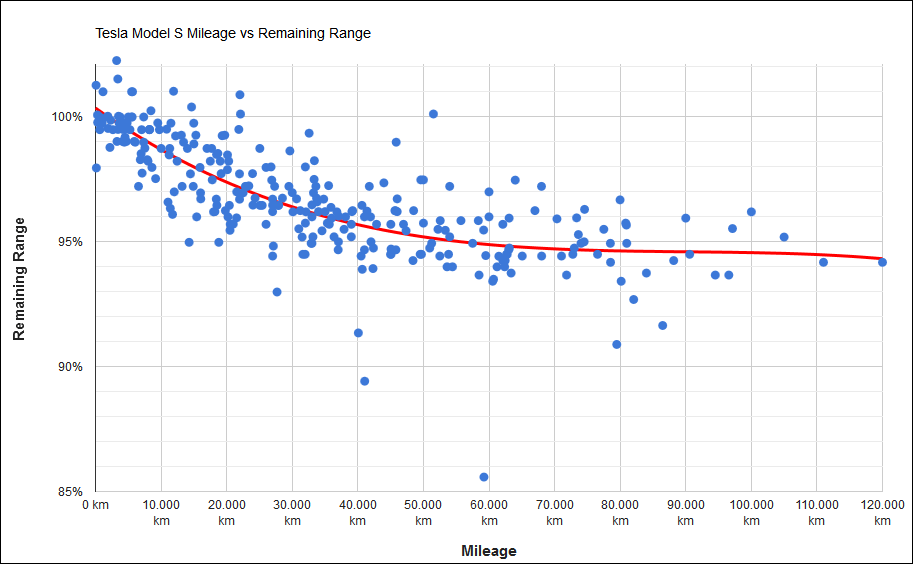
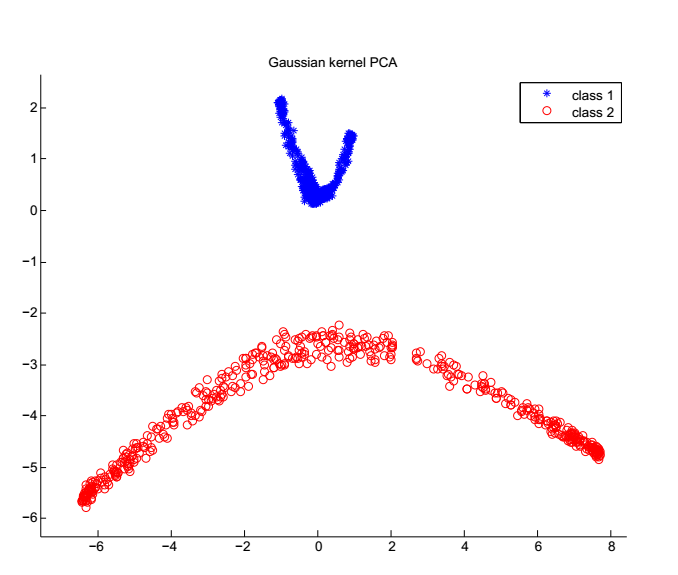
第三章，（K）PCA和判异传统算法的效率比较。在这一章中，我们进行KPCA、PCA和传统的异常值检测的算法的判异效率和优良度比较。我们在这里使用了线性可分的数据——电动汽车的SOC数据，并且用应用标准定义了异常值，分别用这几种算法对数据进行异常值检测，并且计算其检测率和误报率，得出了各个算法的异常值优度比较结果。

第四章，PCA和KPCA在高维数据下的分类性能差异。在这一章中，我们重点论述KPCA和PCA两种算法在面对高维数据进行分类的性能差异，并且把分类结果和异常值检测的原理结合起来，说明了KPCA在面对高维数据时具有性能优势，从而选择KPCA进行高维数据的异常值检测。

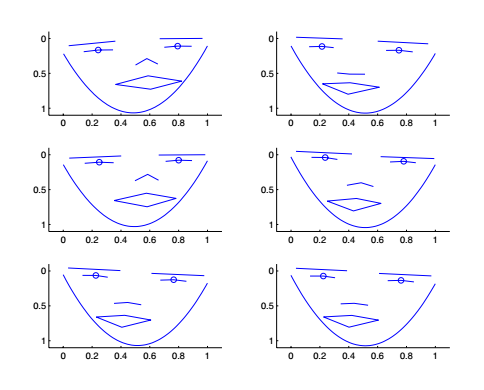
第五章：基于KPCA的异常值检测的主动形状模型。在这一章中，我们使用主要使用人脸数据进行主动形状模型的构建，并且在构建模型之前用基于KPCA的异常值检测排除了不稳定的数据点。在构建了基于高斯核心的主动形状模型之后，我们尝试改变不同参数，观察参数对人脸模型的影响。

第六章：讨论和总结。在这一章中，我们主要讨论了KPCA的高斯核心中模型参数的选择问题，并且对参数变化造成人脸变化做了一个直观的解释。最后，对整个实验过程和论文结论进行了总结。

为了更加明确而清晰的表达本文的实验过程和行文思路，我们在下面给出了技术路线图，如图1.1所示。

主动形状模型

高维人脸数据

各种异常值检测的

方法和思路

问题提出

研究背景及意义

国内外研究现状

研究思路和方法

KPCA和PCA相对传统异常值检测的优势

算法回顾

检验异常值的思想

KPCA相对PCA在

高维数据场景的优势

线性可分数据

特斯拉电池实验

基于KPCA的主动

形状模型

讨论和总结

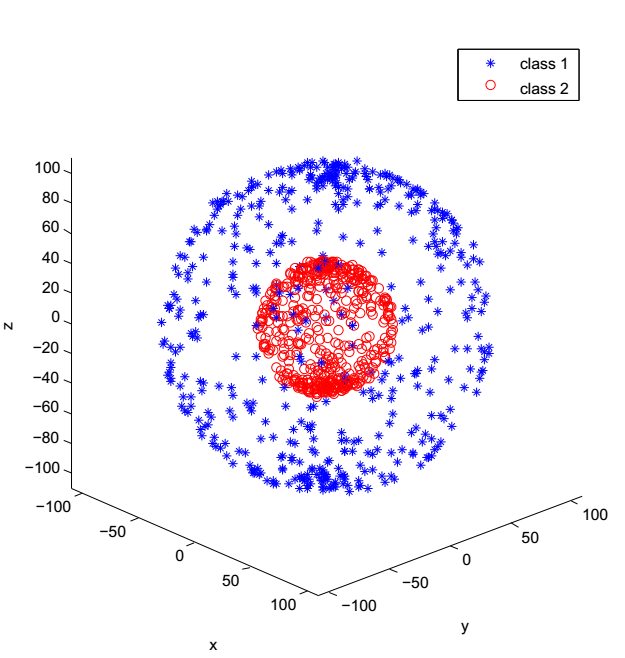
高维同心球数据

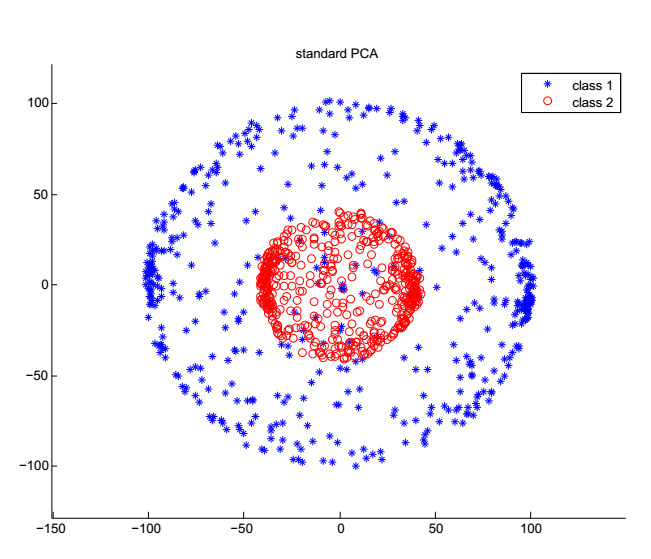
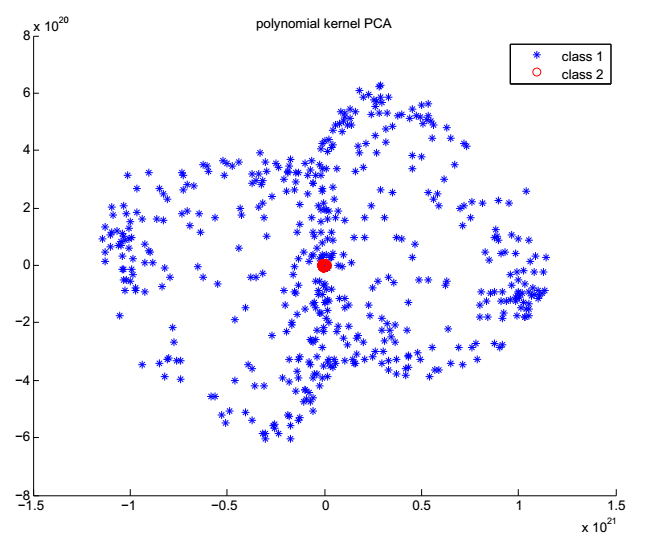
同心球数据分类实验

图1.1 技术路线图

1.4.3 创新点

（1）根据论文思路，我们设计了特斯拉电池数据实验，用实验的异常值检测结果说明了KPCA和PCA相对传统异常值检测方法的优势，并且通过计算检验异常值的准确率和误报率将检测结果表现出来。

（2）通过设计同心球高维数据分类实验，根据实验结果和算法原理论证了KPCA在高维数据场景下相对PCA在异常值检测上更具有优势，并且基于这个结果进行了基于KPCA的异常值检测的应用实验，得到了良好的结果。

第2章 异常值检测的方法

异常值检测作为一个热点话题，有着许多精妙的解决方法，其中包括很多经典的传统方法，当然也包括我们现在用的PCA以及KPCA。通过实验得出结论固然十分重要，但也不能忽视了算法本身的思想，因此我们在这里给出不同异常值检测的思想，先在算法内核上看看他们的特点。

2.1 传统异常值检测的方法

传统常用的异常值检测方法有许多，基于篇幅限制，我们只使用其中三种进行讨论，并基于他们设计实验。

2.1.1 局部距离法

这个算法也叫做局部异常因子算法。

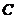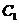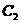如图2.1，它的直观解释是这样的:在一个大集合中，存在两个子集和。其中集合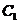中的点的整体距离、密度和分布的情况相比较而言显得均匀，我们认为他们是同一簇； 同样的对于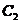中的点我们也可以认为他们是一簇的。而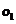和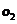两个点是显得相对孤立的，因此可以把他们当成异常点或者说离群点。局部距离法可以在这种存在两个密度分散情况迥异子集下把异常点给识别出来。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：