摘 要

椭圆曲线公钥密码体制的安全是依靠椭圆曲线离散对数问题的不易解的特点保证的，相比于其他公钥加密体制它有着无可比拟的优点，例如在相同的安全级别下，它的密钥长度更小、加解密的速度更快，因此在公钥密码系统中它逐渐地被广泛的使用，如今它已成为公钥密码系统中的一个热门研究对象。

本文主要研究了GF(p)上的椭圆曲线密码体制。首先，介绍了关于椭圆曲线的基本理论知识；接着，设计和实现了椭圆曲线上的ElGamal密码体制，并测量了不同比特长度的p参数下椭圆曲线的加密和解密的效率；同时，实现了RSA密码体制，并与所实现的ElGamal密码体制进行了加密和解密的效率对比。

实验结果表明，椭圆曲线上的ElGamal密码体制的加密和解密时间与参数p的比特长度成正相关；在保证相同的安全程度下，椭圆曲线上的ElGamal密码体制的加密和解密速度慢于RSA密码体制。

关键词：椭圆曲线密码；ElGamal密码体制；RSA密码体制

Abstract

The security of the Elliptic Curve Cryptography is guaranteed by the difficult characteristics of the Elliptic Curve Discrete Logarithm Problem. Compared with other public key cryptosystems, it has unparalleled advantages. For example, under the same security level, its key length is shorter and encryption and decryption is faster. Therefore, it is gradually being widely used in public key cryptosystems. Nowadays, it has become a hot research object in public key cryptosystem.

This paper mainly studies the elliptic curve cryptosystem over GF(p). Firstly, the basic theoretical knowledge about elliptic curve is introduced. Secondly, the ElGamal elliptic curve cryptosystem is designed and implemented, and the efficiency of encryption and decryption of elliptic curve under different p-parameters is measured. At the same time, the RSA cryptosystem is implemented, and its efficiency of encryption and decryption is compared with the ElGamal cryptosystem’s.

The experimental results show that the encryption and decryption time of the ElGamal elliptic curve cryptosystem is positively correlated with the bit length of the parameter p. Under the same security level, the encryption and decryption speed of the ElGamal elliptic curve cryptosystem is slower than the RSA cryptosystem.

Key Words：elliptic curve cryptography; ElGamal cryptosystem; RSA cryptosystem

目 录

第1章 绪论 1

1.1研究背景 1

1.2研究现状 2

1.2.1 国外研究现状 2

1.2.2 国内研究现状 2

1.3 研究内容及意义 3

1.4 文章内容结构 3

第2章 基础知识介绍 4

2.1 群和域 4

2.1.1 群 4

2.1.2 域 4

2.2 欧拉函数 5

2.3 平方剩余 5

2.4 大素数域上的椭圆曲线 6

2.4.1 椭圆曲线的定义 6

2.4.2 椭圆曲线运算规则 7

2.5 椭圆曲线离散对数问题 8

2.6 椭圆曲线离散对数的攻击方式 8

2.6.1 小步大步算法 8

2.6.2 Pollard ρ算法 9

第3章 ECC密码系统中的运算 10

3.1 椭圆曲线上的运算 10

3.1.1 点加运算和倍点运算 10

3.1.2 点乘运算 10

3.1.3 点乘算法的比较 13

3.2 明文数字化中的运算 14

3.2.1 明文信息嵌入到椭圆曲线 14

3.2.2 二次剩余方程的求解 14

3.3 加密解密中的运算 15

第4章 ElGamal密码系统的设计与实现 17

4.1 系统设计 17

4.2 系统实现 17

4.2.1 主要类的结构 17

4.2.2 椭圆曲线层 18

4.2.3 协议层 19

4.3 椭圆曲线参数的选择 19

4.4 加密解密效率与参数p的关系 19

第5章 RSA与ECC的对比 21

5.1 RSA算法的描述 21

5.2 安全性对比 21

5.2 加密与解密效率对比 22

第6章 总结与展望 24

6.1总结 24

6.2展望 24

参考文献 25

致谢 26

绪论

本章主要从研究背景、国内外研究现状、研究内容、研究意义几个方面进行相关的阐述。

1.1研究背景

在如今这个计算机网络深度普及的时代，信息被称为社会发展的重要战略资源，确保信息的安全是信息社会中十分重要的一件事，如何保护信息的安全，防止其被窃取、篡改、破坏，已经成为人们普遍关注的问题。密码技术不失为一种有效可行的技术，同时也是保障信息安全的关键技术。随着一代又一代研究人员对密码学的不懈研究和发展，密码学领域出现了许多重大成果和许多新的研究方向。

如今，公钥密码体系普遍应用于各种加密系统中，其中应用最广泛的RSA公钥密码体制的安全性是依靠大整数因式分解的难解性保证的，但是随着大型计算机的计算能力和计算速度的不断提高，人类已经成功分解了以前被认为是不可能分解的大数，所以为了保证安全性，现代RSA的密钥尺寸至少需要1024比特甚至更多，这就意味着其系统参数所占用的存储空间更多，运算时计算量更大，处理的速度也会变慢。不同于RSA，ECC是基于椭圆曲线离散对数问题(ECDLP)而实现的，从表1.1我们可以看出在相同安全级别下，ECC的密钥尺寸更小，这使得ECC更适合资源受到限制的应用场景，ECC也凭借这一独特的优势逐渐成为密码学研究的热点。为了使ECC被更加广泛的应用，如何完善它的体制，加快它的运行速度，这是密码学研究人员需要解决的重要问题。

表1.1 ECC和RSA同等安全条件下所需密钥长度表

1.2研究现状

自1985年Neal Koblitz和Victor Miller分别独立的提出了椭圆曲线密码理论以来，国内外很多组织和机构都对椭圆曲线密码体制进行了研究，极大的推动了椭圆曲线密码体制的发展和进步。

1.2.1 国外研究现状

随着ECC的快速发展，大量与ECC相关的理论成果和技术产品被研究出来。Certicom公司研发出了用于ECC的集成电路，该产品被应用于网络、通信、商业等众多领域。同时Certicom还与众多知名公司一起建立战略联盟，共同推动ECC的发展与应用，这其中就包括Motorola、Oracle、Sony、Cisco等全球知名的大公司。RSA公司积极的投入到ECC的研发中，并为所研究出的ECC技术申请专利。GlobeSet公司也在研究如何将ECC应用到电子商务和服务中。Sun公司计划推出支持ECC的Java系统网络服务器。

各个国家及其政府机构也积极的参与到ECC的研发与应用中。韩国在其中投入大量人力物力最终取得了骄人的成绩，它研究出的SEED算法在国际中得到了广泛的认可和应用。美国政府已经将椭圆曲线加密算法应用于移动、无线环境中。2005年2月，美国国家安全局(NSA)宣布将ECC作为保护其信息安全和通信安全的公钥密码系统的标准。

几个国际标准化组织制定了许多关于椭圆曲线密码体制的标准。其中IEEE制定的IEEE P1363规定了以ECC为基础的密钥协议与签名算法；美国国家标准与技术研究院(NIST)发布的FIPS PUB 186-4提供了15条安全可靠的椭圆曲线；美国国家标准协会(ANSI)制定了ANSI-X9.62和ANSI-X9.63数字签名标准；ISO制定的ISO/IEC 14888-3标准规定了生成密钥的过程，生成签名的过程以及验证签名的过程。这些标准文档都极大推动了椭圆曲线密码学的发展。

1.2.2 国内研究现状

为了响应国家商用核心密码算法不准采用国外的，必须自主研发的政策，我国的一些科研机构和公司十分重视ECC的理论研究和产品开发，椭圆曲线密码学更是被列为国家重点研究内容。

2010年12月，国家密码管理局发布了《SM2椭圆曲线公钥密码算法》和《SM3密码杂凑算法》。SM2算法作为我国自主研发的一款椭圆曲线密码算法同普通的ECC算法相比有着其独特之处。首先SM2使用的参数不是NIST等国际机构建议的参数，这些参数是由一定的算法产生，这种参数产生方式大大提高了SM2算法的安全性；其次，SM2算法中使用的不是国际通用的Hash算法而是我国自主研发的SM3算法。2012年11月国密局又发布了《SM2密码算法使用规范》，该规范给出了椭圆曲线密码体制的详细实现方式以及推荐的曲线参数。2013年，清华大学的研究团队成功的研究出一款达到国际领先水平的ECC芯片THECC233-100，其安全强度与2048位的RSA相当。2016年3月，国密局发布《SM9标识密码算法》，SM9算法减小了密钥和证书管理的复杂程度，具有使用方便，易于部署的优点。

总的来说，ECC技术是一种非常有前景的技术，国内外的组织和机构都十分看好ECC的发展，相信在不久的将来，ECC将会得到普遍的应用。

1.3 研究内容及意义

本文对有限域椭圆曲线公钥密码体制进行了研究，并实现了ECC的加密和解密。研究的主要内容如下：（1）研究椭圆曲线加密的基础数论知识，主要概念和加密解密的关键算法。（2）实现椭圆曲线加密和解密，并研究其参数对其效率的影响。（3）实现RSA加密解密系统并与ECC进行比较。

本次研究的意义在于，通过实现椭圆曲线加密和解密而充分的理解其原理，并测量不同参数下加密和解密的执行时间来研究不同参数对加密和解密效率的影响，进而能够针对不同的应用环境对参数进行优化。其次，通过和RSA进行效率和安全性对比，研究它们之间的差异性。

1.4 文章内容结构

本文结构如下：

第二章：主要讲解相关的基础数论知识；大素数域椭圆曲线的定义；介绍椭圆曲线离散对数问题(ECDLP)和现阶段对椭圆曲线加密的攻击手段。

第三章： 讲解椭圆曲线密码系统中所涉及到的运算，如：椭圆曲线上的点加运算，点乘运算，倍点运算等。

第四章：对椭圆曲线上的ElGamal密码体制进行设计和实现，并对不同参数下它的加密和解密的效率进行测量。

第五章：设计和实现RSA密码系统，并与ECC进行对比。

第六章：对文章总结并对未来工作进行展望。

第2章 基础知识介绍

本章对相关理论知识进行了介绍。首先介绍了密码学中的常用数学知识：群、域和欧拉函数等，然后介绍了素数域的椭圆曲线的相关定义，最后对椭圆曲线加密的安全性和攻击方式进行了简要介绍。

2.1 群和域

2.1.1 群

定义2-1^[1] 对于一个集合G以及定义在该集合上的一个运算*，且运算*满足以下条件：

（1）G上的运算*满足封闭性，即如果a, b是G中的任意两个元素，那么运算a * b的结果也在G中；

（2）G上的运算*满足结合律，即对G中的元素a, b, c，有(a * b) * c = a * (b * c)；

（3）存在一个元素e，对于G中的任意一个元素a，都有a * e = e * a = e；e称为lt;G, *gt;的单位元；

（4）每一个元素都存在运算*上的逆元，即对G中的任意一个元素a，都存在元素a^-1，使得a * a^-1 = a^-1 * a = e；称a^-1为元素a的逆元。

则称lt;G, *gt;是群。

如果G含有有限个元素，则称lt;G, *gt;是有限群，否则是无限群。有限群中，G含有的元素个数称为群的阶数。

如果群lt;G, *gt;中的*运算还满足交换律，即对G中的任意两个元素a, b，都有a * b = b * a，则称lt;G, *gt;为交换群或Abel群。

设lt;G, *gt;是一个群，I是一个整数集合，如果gG，对于aG都iI，使得a = gⁱ，则称lt;G, *gt;是循环群，g称为循环群的生成元。

2.1.2 域

定义2-2^[1] 若代数系统lt;F, , *gt;的二元运算加法 和乘法*满足：

（1）lt;F, gt;是交换群；

（2）F中的非零元素构成*运算上的Abel群，其中0是 的单位元；

（3）乘法*在加法 上满足分配律，即对a, b, cG，有a *(b c) = a * b a * c 和

(b c) * a = b * a c * a

则称lt;F, , *gt;是域。

有限域是指域中所含的元素个数有限的域，元素的个数称为该域的阶。若q是素数的自然数幂，则阶为q的域称为Galois域，记为GF(q)^[1]。

在椭圆曲线加密中常用的两种有限域是大素数域GF(p)和二进制域GF(2^m)，本文实现的是大素数域上的椭圆曲线加密解密系统，所以后面将会对大素数域的椭圆曲线进行简单的介绍。

2.2 欧拉函数

定义2-3^[1] 设n是正整数，比n小且与n互素的正整数的个数称为n的欧拉函数，记为φ(n)。

φ(n)的计算规则如下：

（1）若n是素数，则

（2）若n = pq，其中p，q是素数，则

（3）若n有标准分解式n = …，则

2.3 平方剩余

定义2-4^[1] 设p，是正整数，且和p互素，如果方程

有解，则称是模p的二次剩余，否则称为二次非剩余。

可以通过计算Legendre符号来判断a是否是p的平方剩余，当p是素数时的定义如下：

此时Legendre符号的计算公式如下：

2.4 大素数域上的椭圆曲线

2.4.1 椭圆曲线的定义

人们为了研究椭圆积分 (E(x)为x的三次或四次多项式)而引入了椭圆曲线的概念，一般地，椭圆曲线是以下等式所描述的维尔斯特拉斯方程所确定的平面曲线：

其中，，，，是满足某些条件的实数，定义还包括一个称为无穷远点的元素，记为O^[1]。

如果方程定义式（2-6）中的系数，，，，都属于有限域GF(P)（p为一个大素数），那么就称该曲线为大素数域上的椭圆曲线，最常见的是由方程

所确定的曲线，其中判别式。

素数域上的椭圆曲线并不是一条连续的曲线而是一个个离散的点，有素数域上的椭圆曲线y2=x3 x 1 (mod 23)的图像如下图所示：

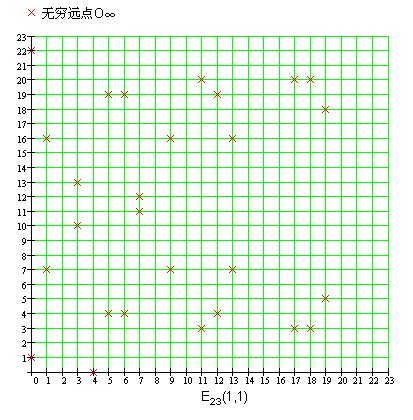
图2.1 y2=x3 x 1 (mod 23)的图像

2.4.2 椭圆曲线运算规则

如果一条直线与椭圆曲线相交，交点个数为n，那么这n个点的和为O，根据该规则我们可以得到椭圆曲线上的加法法则：

（1）加法单位元为无穷远点O，即对于椭圆曲线上任意一点P，等式O P = P成立；

（2）如图2.2，椭圆曲线上一点的加法逆元为，因为三点位于一条直线上，所以有，即；

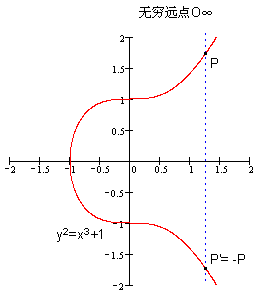
图2.2 椭圆曲线逆元示意图